М-метод

Математическая модель КЗ

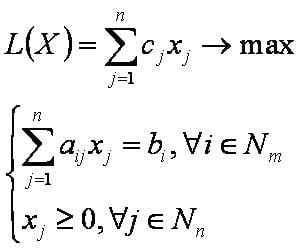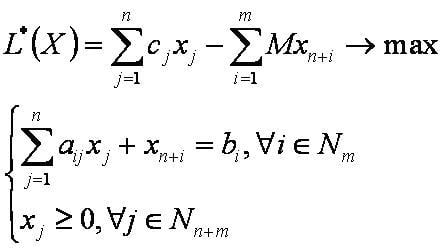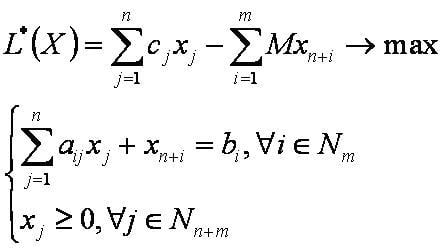
Математическая модель эквивалентной КЗ

M-метод — метод решения задач линейного программирования канонического вида, то есть задач с ограничениями в форме равенств.

Описание метода

Суть M-метода состоит в построении с помощью искусственных переменных эквивалентной задачи с базисом, а затем решении её симплекс-методом.

Каноническая задача

Математическая модель канонической задачи имеет следующий вид:

$L(X)=\sum \limits _{j=1}^{n}c_{j}x_{j}\rightarrow \max$

${\begin{cases}\sum \limits _{j=1}^{n}a_{ij}x_{j}=b_{i},\ \forall i\in N_{m}\\x_{j}\geq 0,\forall j\in N_{n}\end{cases}}$

или

$L(X)=c_{1}x_{1}+c_{2}x_{2}+\ldots +c_{n}x_{n}\rightarrow \max$

${\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}=b_{2}\\\ldots \\a_{m1}x_{1}+a_{m2}x_{2}+\ldots +a_{mn}x_{n}=b_{m}\\x_{1}\geq 0,\ x_{2}\geq 0,\ldots ,\ x_{n}\geq 0\end{cases}}$

Постановка эквивалентной задачи

Для решения задачи канонического вида необходимо составить эквивалентную задачу. Введём новые (искусственные) переменные x_j — остатки ресурсов (j-n)-го ограничения, j=n+1,n+2,…,n+m. Добавим эти переменные к соответствующим ограничениям и введём их в целевую функцию с отрицательным коэффициентом -M, где M — очень большое положительное число.

Математическая модель эквивалентной задачи принимает следующий вид:

$L^{*}(X)=\sum \limits _{j=1}^{n}c_{j}x_{j}-\sum \limits _{i=1}^{m}Mx_{n+i}\rightarrow \max$

${\begin{cases}\sum \limits _{j=1}^{n}a_{ij}x_{j}+x_{n+i}=b_{i},\ \forall i\in N_{m}\\x_{j}\geq 0,\forall j\in N_{n+m}\end{cases}}$

или

$L(X)=c_{1}x_{1}+c_{2}x_{2}+\ldots +c_{n}x_{n}-$

$-Mx_{n+1}-Mx_{n+2}-\ldots -Mx_{n+m}\rightarrow \max$

${\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}+x_{n+1}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}+x_{n+2}=b_{2}\\\ldots \\a_{m1}x_{1}+a_{m2}x_{2}+\ldots +a_{mn}x_{n}+x_{n+m}=b_{m}\\x_{1}\geq 0,\ x_{2}\geq 0,\ldots ,\ x_{n+m}\geq 0\end{cases}}$

Метод решения

Эквивалентная задача решается симплекс-методом.

Начальная симплекс-таблица для эквивалентной задачи имеет вид:

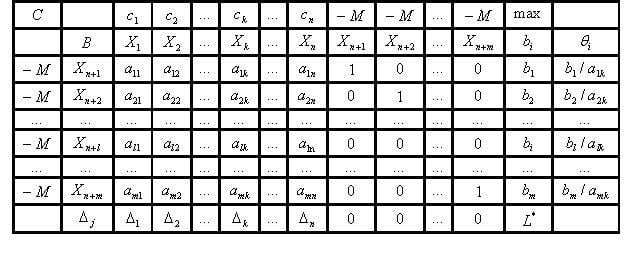
Если оптимальное значение целевой функции эквивалентной задачи не содержит M-множителей, то получено оптимальное решение, которое при отбрасывании искусственных переменных совпадает с оптимальным решением исходной задачи канонического вида. В случае если оптимальное значение целевой функции эквивалентной задачи содержит M-множители, то это означает несовместность системы ограничений исходной задачи канонического вида и отсутствие допустимых решений.

Другие методы

• Симплекс-метод;
• Метод искусственного базиса.

Литература

• Юдин Д. Б., Гольштейн Е. Г. Линейное программирование. — М., 1963.