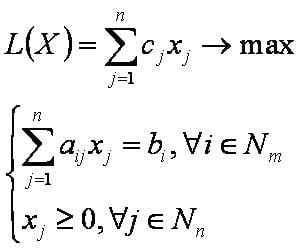Каноническая задача линейного программирования

Математическая модель КЗ

Каноническая задача — это основная задача линейного программирования канонического вида, т.е. задача с ограничениями в форме равенств.

Математическая модель

Математическая модель канонической задачи имеет следующий вид:

$L(X)=\sum \limits _{j=1}^{n}c_{j}x_{j}\rightarrow \max$

${\begin{cases}\sum \limits _{j=1}^{n}a_{ij}x_{j}=b_{i},\ \forall i\in N_{m}\\x_{j}\geq 0,\forall j\in N_{n}\end{cases}}$

или

$L(X)=c_{1}x_{1}+c_{2}x_{2}+\ldots +c_{n}x_{n}\rightarrow \max$

${\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}=b_{2}\\\ldots \\a_{m1}x_{1}+a_{m2}x_{2}+\ldots +a_{mn}x_{n}=b_{m}\\x_{1}\geq 0,\ x_{2}\geq 0,\ldots ,\ x_{n}\geq 0\end{cases}}$

Метод решения

Каноническая задача решается М-методом, также для решения может применяться метод искусственного базиса и симплекс-метод.

Другие задачи:

• Производственная задача;
• Общая прямая задача линейного программирования;
• Общая двойственная задача линейного программирования;
• Классическая транспортная задача;
• Распределительная задача;
• Задача о назначениях;
• Транспортная задача с промежуточными пунктами;
• Трёхиндексная транспортная задача;
• Задача целочисленного программирования;
• Задача о рюкзаке.

Литература

• Юдин Д. Б., Гольштейн Е. Г. Линейное программирование — М.,1963.