Тригонометрические функции, их графики
Функция синуса[править]
Функция синуса имеет вид:
.
Основные свойства этой функции:
- Область определения ;
- Область значений ;
- Функция нечётная ;
- Функция не является монотонной на всей своей области определения;
- Функция периодична с периодом .
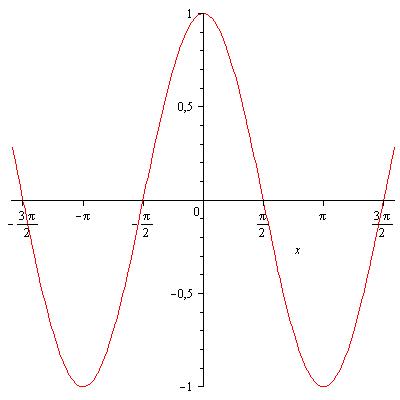
Синусоида[править]
Синусо́ида — плоская кривая, задаваемая в прямоугольных координатах уравнением
Построение графика удобно начинать с изображения области, которая ограничивает график сверху числом 1 и снизу числом -1, что обусловленно областью значений функции.
Также важно помнить значения синусов нескольких основных табличных углов, что позволит построить первую полную «волну» графика и потом перерисовывать её вправо и влево с периодом .
Функция косинуса[править]
Функция косинуса имеет вид:
.
Основные свойства этой функции:
- Область определения ;
- Область значений ;
- Функция чётная ;
- Функция не является монотонной на всей своей области определения;
- Функция периодична с периодом .
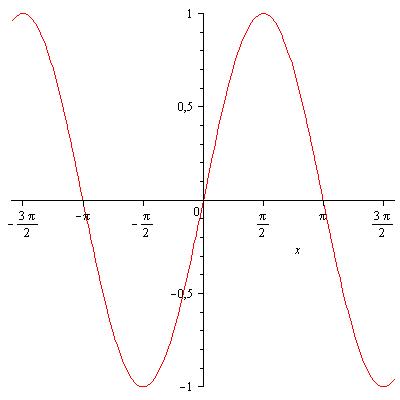
Косинусоида[править]
Косинусо́ида — плоская кривая, задаваемая в прямоугольных координатах уравнением
- .
Построение графика косинуса также удобно начинать с изображения области, которая ограничивает график сверху числом 1 и снизу числом -1, в соответствии с областью значений функции.
Полезно помнить значения косинусов нескольких основных табличных углов, что позволит построить первую полную «волну» графика и потом перерисовывать её вправо и влево с периодом .
Функция тангенса[править]
Функция тангенса имеет вид:
.
Основные свойства этой функции:
- Область определения , кроме (тангенс этих аргументов не существует);
- Область значений ;
- Функция нечётная ;
- Функция монотонно возрастает в пределах своих так называемых веток тангенса (см. рис.);
- Функция периодична с периодом .
Тангенсоида[править]
Построение графика функции удобно начинать с изображения вертикальных асимптот графика в точках, которые не входят в область определения, то есть и т. д.
Далее изображаем ветки тангенса внутри каждой из образованных асимптотами полос, прижимая их к левой асимптоте и к правой. При этом не забываем, что каждая ветка монотонно возрастает.
Все ветки изображаем одинаково, так как функция имеет период, равный . Это видно по тому, что каждая ветка получается смещением соседней на вдоль оси абсцисс.
Функция котангенса[править]
Функция котангенса имеет вид:
.
Основные свойства этой функции:
- Область определения , кроме (котангенс этих аргументов не существует);
- Область значений ;
- Функция нечётная ;
- Функция монотонно убывает в пределах своих веток, аналогичных веткам тангенса (см. рис.);
- Функция периодична с периодом .
Котангенсоида[править]
Как и для тангенса, построение удобно начинать с изображения вертикальных асимптот графика в точках, которые не входят в область определения, то есть и т. д. Далее изображаем ветки котангенса внутри каждой из образованных асимптотами полос, прижимая их к левой асимптоте и к правой. В этом случае учитываем, что каждая ветка монотонно убывает. Все ветки аналогично тангенсу изображаем одинаково, так как функция имеет период, равный .
Вычисление периодов тригонометрических функций со сложным аргументом[править]
У тригонометрических функций со сложным аргументом период может быть нестандартным.
Например, у функций:
- и
период будет равен:
.
Для функций:
- и
период составляет
.
Как можно заметить, новый период получается делением стандартного периода на множитель при аргументе. От других видоизменений функции он не зависит.
Ссылки[править]
- «Что такое синус и синусоида» — перевод статьи Intuitive Understanding of Sine Waves | BetterExplainedангл.
Одним из источников, использованных при создании данной статьи, является статья из википроекта «Рувики» («ruwiki.ru») под названием «Тригонометрические функции, их графики», расположенная по адресу:
Материал указанной статьи полностью или частично использован в Циклопедии по лицензии CC-BY-SA 4.0 и более поздних версий. Всем участникам Рувики предлагается прочитать материал «Почему Циклопедия?». |


![{\displaystyle E(y)=[-1;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfe43c8076e923b7c300400de3cf60a9f4b738d2)