Вселенная в точке

Вселенная в «точке» — утверждаемая Климцом А. П. возможность размещения пространств любой протяженности в многомерной «точке» с заданным размером (то есть в малой области многомерного пространства), в том числе свободного размещения всей нашей Вселенной в многомерной «точке» диаметром 10⁻³³ см.

Вводные утверждения

Одной из трудностей общей теории относительности является проблема сингулярностей, которая фактически возникла с момента получения Фридманом нестационарных космологических решений уравнений общей теории относительности и еще более обострилась в связи с задачей о релятивистском гравитационном коллапсе. Сингулярность обозначает состояние бесконечной плотности материи, что свидетельствует о недостаточности общей теории относительности.

По космологической модели, процесс эволюции в направлении к особой точке (сингулярности) складывается из последовательных серий колебаний, в течение каждой из которых расстояния вдоль двух пространственных осей осциллируют, а вдоль третьей — монотонно убывают, объем убывает по закону, близкому к $\sim t$. Последовательная серия колебаний сгущается по мере приближения к особой точке. Весь процесс приближения к особой точке растянут до бесконечности.

Говоря об особой точке, имеют в виду физическую особенность — обращение в бесконечность плотности материи и инвариантов тензора четырехмерной кривизны. Особенность, которую имеет решение Фридмана, характерна тем, что обращение в нуль пространственных расстояний происходит по одинаковому закону во всех направлениях. Такой тип особенности не является достаточно общим: он свойствен классу решений, содержащему лишь три произвольные функции координат. Эти решения существуют только для пространства, заполненного материей. Особенность же колебательного типа имеет общий характер — существует решение уравнений Эйнштейна с такой особенностью, содержащее всю требуемую совокупность произвольных функций координат. Существование особой точки во времени является весьма общим свойством решений уравнений Эйнштейна, причем режим приближения к особой точке имеет в общем случае колебательный характер. Этот характер не связан с наличием материи (а потому и с ее уравнением состояния) и свойствен уже самому по себе пустому пространству-времени. Зависящая от присутствия материи особенность монотонного изотропного типа, свойственная решению Фридмана, имеет лишь частное значение.

Говоря об особенностях в космологическом аспекте, имеют в виду особую точку, достигаемую всем пространством, а не лишь его ограниченной частью, как при гравитационном коллапсе конечного тела. Такой же характер имеет и особенность, достигаемая конечным телом в его коллапсе под горизонтом событий в сопутствующей системе отсчета. Отбор решения, отвечающего реальному миру, связан с физическими требованиями, установление которых на основании одной лишь существующей теории гравитации невозможно, и которые смогут быть выяснены в результате дальнейшего синтеза физических теорий. Этому отбору соответствует какой-либо частный (например, изотропный) тип особенности.

По мнению А.П. Климца многомерие решает эти проблемы. При этом исчезает проблема бесконечной плотности материи и, соответственно, инвариантов тензора четырехмерной кривизны.

Как разместить Вселенную в «точке»

Для книги, как примера 3-мерного объекта, количество информации в виде букв занимает в книге объем V.

Если это же количество информации разместить в 2-мерном пространстве, то есть на плоскости, то в виде строк информация займет площадь S со стороной квадрата $a(2)$, причём $a(2)>a(3)$, где $a(3)$ — сторона 3-мерного куба, изображающего книгу.

Это же количество информации, помещенное в одномерное пространство, в виде строки раcтянется в длину величиной $a(1)$, причем

$a(1)>a(2)>a(3)$

При увеличении числа измерений пространства для размещения одного и того же количества информации (в виде букв) потребуется n-мерный куб со все меньшей стороной $a(n)$ соответствующего n-мерного куба, то есть

$a(1)>a(2)>\cdots >a(k)>\cdots >a(n)$

При этом $a(n)$ и $a(k)$ связаны соотношением

$a(n)=a(k)^{k/n}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)$

Это уравнение Климца для сингулярностей.

(1) следует из равенства объемов информации (или вещества) в том или ином n-мерном пространстве

$V(1)=V(2)=V(k)=\cdots =V(n)$

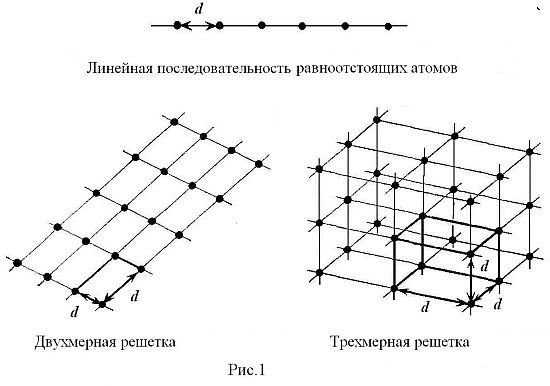
где $V(n)$ — «объемы» n-мерных пространств, заключающих в себе одинаковое (равное) количество единиц информации (или единиц вещества — атомов), расположенных в узлах n-мерных кубических решеток с шагом $d$ в том или ином n-мерном пространстве. Можно представить, что расстояние $d$ между частицами (атомами) становится все меньше и меньше. Цепочки частиц в направлении каждой координатной оси переходят в то, что мы называем континуумом. И наши ряды атомов превращаются в сплошные линии $V(1)$, плоскости $V(2)$, объемы $V(3)$ и т. д. до $V(n)$ (рис.1).

И так как

$V(1)=a(1)^{1};V(2)=a(2)^{2};\cdots ;V(k)=a(k)^{k};\cdots ;V(n)=a(n)^{n};$

то отсюда и следует (1). Здесь, например, $a(1)=d\cdot t$, где $t$ — число шагов решетки.

Для 3-мерного пространства из (1)

$a(n)=a(3)^{3/n}\,\,\,\,\,\,\,\,(2)$

Из соотношения (2) следует вывод: если необходимо разместить всю наблюдаемую Вселенную вместе с веществом в элементарном n-мерном «кубике» со стороной $a(n)$, равной величине $10\cdot 10^{-33}cm=10\cdot \ell _{P}$ (то есть десяти единицам планковской длины), где $\ell _{P}=10^{-33}cm$ — одна единица планковской длины.

Размер наблюдаемой Вселенной равен $10^{28}$ см. или, в единицах планковской длины, $10^{61}\ell _{P}$ планковских единиц длины. Из соотношения (2) имеем

$10^{1}\ell _{P}=(10^{61}\ell _{P})^{3/n}\,\,\,\,\,\,\,\,(3)$

Отсюда n = 183. Из (3) видно, что уже при 183 измерениях пространства всю наблюдаемую Вселенную можно разместить в 183-мерном «кубике» со стороной $10\ell _{P}$, то есть фактически в «точке» (183-мерной).

Плотность вещества в таком «кубике» остается равной плотности вещества, находящегося в 3-мерном пространстве наблюдаемой Вселенной. Действительно, плотность вещества в n-мерном пространстве определяется следующим образом: $\rho (n)=M/V(n)$, где $M$ — масса вещества наблюдаемой Вселенной, $V(n)$ — объем n-мерного пространства, $\rho (n)$ — плотность вещества в n-мерном пространстве. И так как, по условию, $V(3)=V(183)$, то и $\rho (3)=\rho (183)$.

Наглядный пример: сворачивание одномерной нити длиной $r_{1}$ в плоский двухмерный «коврик» в виде спирали диаметром $r_{2}$ или в трехмерный клубок диаметром $r_{3}$. Ясно, что $r_{1}>r_{2}>r_{3}$, то есть компактность размещения нити растет с увеличением размерности пространства, однако плотность размещения вещества нити остается прежней (атомы вещества нити по прежнему будут расположены на расстоянии d друг от друга в направлении каждой $n$-ой координатной оси, (см. рис.1).

Если рассматривать не многомерный "куб" а, например, многомерный "шар" и т.п., то уравнение (1) справа нужно умножить на соответствующий коэффициент.

В теории тяготения Ньютона в качестве «точки» по отношению к Солнцу принимается планета Земля и другие планеты. Или, например, в «Фейнмановских лекциях по физике» в § 5 «Всемирное тяготение» говорится «Одно из красивейших небесных зрелищ — шаровое звездное скопление. Каждая точка — это звезда». В физике материальная точка — физическое понятие (модель, абстракция), представляющее тело или область пространства, размерами (и формой) которого можно пренебречь в условиях данной задачи. Здесь пишется слово «точка» в кавычках и определяется это понятие как малая область пространства, хотя это понятие и является относительным и зависит от масштаба поставленной задачи. В данной статье «точка» — это область из 10 планковских единиц. В математике же точка нульмерна, не имеет размера и потому не имеет отношения к статье.

При коллапсе черных дыр при достижении веществом черной дыры определенной (например, планковской?) плотности коллапсирующее вещество в центре черной дыры (в сингулярности) с помощю режима колебательного характера приближения к особой точке выдавливается в иные измерения пространства, которые могут быть свернуты (компактифицированы, зациклены) в кольца диаметром порядка планковской длины.

Согласно соотношению неопределенностей $\Delta R_{\mu }\Delta x_{\mu }\geq \ell _{P}^{2}$, в вакууме на планковском уровне существуют флуктуации геометрии и топологии пространства. В этом масштабе геометрия и топология пространства принимает различные конфигурации, каждая из которых имеет свою амплитуду вероятности $\psi$. Эти амплитуды вероятностей сравнимы по величине для целого диапазона геометрий (с различными размерностями метрических и, соответственно, топологических пространств), ограничиваемого значениями $\Delta g\sim \ell _{P}^{2}/L^{2}$. Этот диапазон геометрий в субмикроскопичеких масштабах столь разнообразен, что его нельзя свести к одной какой-либо 4-геометрии и и топологии. Коллапсирующее вещество в субмикроскопической сингулярности благодаря флуктуациям геометрии и топологии всегда найдет микропространство подходящей размерности для своего компактного размещения.

Развитие

На основе выкладок Климца А. П. Трофименко А. П. была высказана идея, что земные чёрные дыры представляют топологические особенности в структуре околоземного пространства-времени.

По мнению Трофименко А. П. это означает многомерность пространства и времени земных объектов, наличие мостов (туннелей) в параллельные миры прямо на Земле.

Учитывая возможность компактификации с помощью высших размерностей земных тел (вплоть до планковских размеров) с сохранением их обычной плотности, Трофименко А. П. делает вывод о возможности проникновения человека и его технических аппаратов (плотность вещества объектов при многомерной компактификации может не меняться) через многомерные земные чёрные дыры в другие миры (метагалактики), «стартуя» прямо с Земли. Применительно к проблеме космических цивилизаций это означает возможность смены пространственной экспансии цивилизации в трехмерном пространстве выходом сверхцивилизации в высшие размерности Вселенной.

Проверяемость

Положения, позволяющие уяснить проверяемость и/или фальсифицируемость возможности размещения пространств любой протяженности в многомерной «точке» с заданным размером — А. П. Климцом не сформулированы.