Пространство (многомерная модель)

Материал из Циклопедии
Перейти к навигации Перейти к поиску
← другие значения

Пространство (многомерная модель) — наглядная модель многомерного пространства, отображающая свойства пересечений многомерных пространств в трактовке Климца А.П.

Модель раскрывает некоторые необычные стороны многомерных пространств.[1][2]

Философия многомерного пространства[править]

Любой процесс измерения представляет собой, по сути, внешнее отношение одних измеряемых тел или процессов с другими материальными телами или процессами, выступающими в качестве средств измерения (часы, линейки, любые приборы и т. п.).

Внешний характер пространственных измерений наложил отпечаток на формирование соответствующих естественно-математических понятий. В частности, это выразилось в представлении о трехмерности пространства. Реальные вещи, тела, процессы, с которыми сталкивается человек в практической деятельности, объемны. По существу, объемность (или емкость) и представляет собой реальную пространственную протяженность. Пространство не может быть чем-то иным, нежели совокупностью кубических метров. Однако выражение реального объема именно в кубических метрах (сантиметрах, километрах и т. п.) явилось результатом длительного развития прежде всего хозяйственной, но вместе с ней и научной практики. Потребность в измерении посевных площадей, расстояний, на которые перегонялись стада, совершались перекочевки или уходили охотники, собственно говоря, и привела к тому, что исходной основой пространственных измерений явилась длина и ее абстрактное выражение — линия.

Объем в геометрии Евклида трёхмерен потому, что в его основе лежит линия, взятая одномерно; линии образуют двухмерную плоскость, а из плоскостей строится трехмерный объем. Хотя такой путь оптимален и в наибольшей степени удовлетворяет потребности практики, он все же не является единственно возможным. Данные археологии подтверждают, что единицы измерения объема (емкости) исторически являются столь же древними, как и естественные единицы измерения времени и длины (день, месяц, ступня и т. п.). Можно предположить, что если бы практические потребности первобытных людей выдвинули на передний план не измерение площадей и расстояний, а измерение объемов, то развитие геометрической науки могло бы пойти по пути, отличному от проложенного Евклидом. Говорят, к примеру: такая-то комната (пещера, храм, дом, зал и т. д.) больше, чем другая; новый прибор (машина) более компактен и занимает меньше места (меньшее пространство), чем прежняя модель. При всей приблизительности приведенных сравнений реальная пространственная объемность выражена здесь в одном измерении: в отношении «больше — меньше». Если на основе подобных или аналогичных сравнений выработать единицы измерения одномерных объемов и положить их в основу некоторой воображаемой геометрии, то понятие линии в ней могло бы быть совершенно иным: например, выраженным в трех измерениях, скажем как корень третьей степени из единицы одномерного объема. Хотя подобное представление на первый взгляд и кажется вычурным, в действительности в нем нет ничего необычного. При измерении линейкой поверхности стола одномерная линия получается не при помощи операций с двумя объемами (поскольку объемны и линейка, и стол, поверхность которого как сторона реальной объемности подвергается измерению)? Полученная линия и измеренная длина, а также их численные величины и являются результатом определенного сопоставления реальных объемных предметов.

Ни двух-, ни трех-, ни четырехмерность, ни какая-либо другая многомерность не тождественны реальной протяженности, а отображают определенные аспекты тех объективных отношений, в которых она может находиться. Материальный мир — это и мир Евклида, и мир Лобачевского, и мир Римана, и мир Минковского, ибо в понятиях любой из геометрий, связанных с именами этих выдающихся ученых, можно описать и отразить реальную пространственную протяженность как всеобщий атрибут материальной действительности.[3]

Модель многомерного пространства[править]

В трехмерном пространстве справедлива теорема Пифагора

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r^2=x^2+y^2+z^2\,\,\,\,\,\,\,\,\,\,(1)}

где Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r}  — расстояние между любыми двумя точками пространства. Известно, что все содержание эвклидовой геометрии можно вывести из соотношения Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (1)} . Действительно, например, в геометрии Декарта теорема Пифагора является аксиомой.

Рассмотрим множество, состоящее из трех точек (рис.Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 1} ). Здесь точки являются символами, элементами множества. Вместо трех точек можно нарисовать, например, трех крокодилов.

Image1.gif

Поставим в соответствие множеству размерностей Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерного пространства множество точек. Тогда Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерное пространство соответствует множеству из трех точек, Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2} -мерное — множеству из двух точек, Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 1} -мерное — множеству из одной точки, Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 0} -мерное — пустому множеству точек.

Рассмотрим пересечения подмножеств точек в множестве из трех точек (рис.Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2} )

Image2.gif

Напомним, что пересечением называется подмножество, принадлежащее обоим пересекающимся подмножествам. На рис.Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2} пересекаются подмножества, каждое из которых состоит из двух точек. Как видно, подмножества из двух точек могут пересекаться по одной точке. В Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерном пространстве это соответствует пересечению двух Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2} -мерных плоскостей, пересекающихся по Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 1} -мерной прямой.

Рассмотрим рис.Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} . Здесь пересечение двух подмножеств из двух точек и одной точки происходит по пустому множеству точек.

Image3.gif

В Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерном пространстве это соответствует пересечению Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 1} -мерной прямой и Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2} -мерной плоскости в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 0} -мерной точке.

Аналогично можно рассмотреть пересечения в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2} -мерном пространстве и Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 1} -мерном пространстве. Соответствие между множеством точек и множеством размерностей будет полное.

Рассмотрим теперь множество из четырех точек, что соответствует Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 4} -мерному пространству (рис.Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 4} )

Image4.gif

Как видно, в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 4} -мерном пространстве две Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2} -мерные плоскости могут пересекаться по Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 0} -мерной точке, что невозможно сделать в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерном пространстве. Это можно представить наглядно, если спроецировать Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 4} -гранный угол на плоскость аналогично проецированию Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -гранного угла на плоскость и вообразить, что все углы в вершине Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 4} -гранника являются прямыми. В таком Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 4} -граннике любые две противоположные грани (координатные плоскости) пересекаются в одной точке. Никто ведь не удивляется тому, что в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерном пространстве Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} координатные плоскости пересекаются в одной Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 0} -мерной точке.

Из рис.Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2} и рис.Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} становится понятно, почему психологически нельзя представить в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерном пространстве пересечение двух плоскостей в одной точке. Мы живем в пространстве Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -х измерений и выйти в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 4} -ое измерение не можем. Любые комбинации пересечений подпространств в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -ом пространстве не приведут к пересечению двух плоскостей в одной точке (см. рис.2). Ведь они должны пересечься по пустому множеству точек, что невозможно.

Вообще, если рассмотреть множество из Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n} точек, что соответствует Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n} -мерному пространству, то легко обнаружить, что выполняется следующее соотношение

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle l\ge m+k-n\,\,\,\,\,\,\,\,\,\,(2)}

где Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle l}  — подмножество точек в пересечении подмножеств Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} и Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle k} ; Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n}  — все множество точек.

В теории конечномерных векторных пространств существует аналогичное соотношение

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dim l\ge \dim m+\dim k-\dim n\,\,\,\,\,\,\,\,\,\,(3)}

где dimension — «размерность»; Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dim l}  — размерность подпространства, получаемого в результате пересечения подпространств Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} и Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle k} ; Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dim n}  — размерность объемлющего пространства.[4]

Пусть мы имеем бесконечномерные пространства Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle M} и Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle K} . Тогда в нашей модели их пересечение отобразится подмножеством Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle L} из бесконечного числа точек (рис.Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 5} )

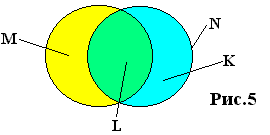
Image5-1.gif

то есть сплошной непрерывной областью. Уравнения Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (2)} и Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (3)} будут здесь иметь вид

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle L\ge M+K-N}

Рассмотрим теперь множество из Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 9} точек, что соответствует Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 9} -мерному пространству (рис.Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 6} )

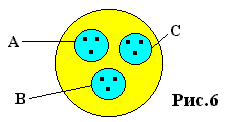
Image6.gif

Если это множество разбить на подмножества по три точки — Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B} , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C} , то нетрудно видеть, что пересечения подмножеств Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B} , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C} аналогично пересечениям подмножеств из трех точек. В Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 9} -мерном пространстве это означает, что три его Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерных подпространства могут пересекаться в одной точке и быть взаимно ортогональными. Таким образом, Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерное подпространство в этом случае может играть роль координатной «оси». Здесь обобщается и понятие угла между такими «осями». Тогда то, что соответствует Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2} -мерным плоскостям в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерном пространстве, здесь будет Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 6} -мерным подпространством.

Мы взяли по три точки в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B} , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C} только в качестве примера. Пусть в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B} , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C} будет по Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n} точек. Тогда мы получим аналог Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3\,n} -мерного пространства. «Куб», например, в таком пространстве может выглядеть следующим образом (рис.Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 7} )

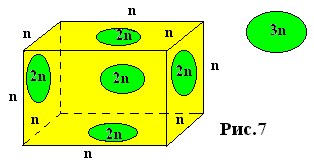
Image7.gif

Здесь каждое ребро Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n} -мерно, каждая грань Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2\,n} -мерна, сам куб Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3\,n} -мерен, но точечных вершин будет восемь. Если в качестве «линии» в Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3\,n} -мерном пространстве взять его Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n} -мерное подпространство, то мы получим с таким определением обычную Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерную геометрию, где каждая точка может быть охарактеризована тремя числами по отношению к Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n} -мерным координатным «осям». Единственное отличие от Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерного пространства будет состоять в том, что «длина» этой «линии» будет измеряться метрами в степени Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n} (см, км, и т. п.). т.е. Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mu^n} . Теорема Пифагора в этом случае будет иметь вид

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r^2_{\mu^{2n}}=x^2_{\mu^{2n}}+y^2_{\mu^{2n}}+z^2_{\mu^{2n}}}

При таком определении такая «Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерная» геометрия формально ничем не будет отличаться от Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерной геометрии Евклида со всем ее содержанием.

В принципе Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n} можно устремить к бесконечности и мы получим «Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерную» геометрию с бесконечным числом внутренних степеней свободы. «Точки» в таком пространстве (то есть очень малые области) будут бесконечномерными.

Мы приходим к выводу, что даже если наблюдатели пользуются формализмом Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3} -мерной геометрии, само пространство может быть в изложенном выше смысле много- и даже бесконечномерным, но дополнительные измерения пространства ненаблюдаемы (например, свёрнуты в кольца с планковским радиусом).

Интересно отметить, что эта статья пересекается со статьей [5], где поясняются такие понятия многомерной алгебры, как множества, морфизмы, категории, кобордизмы, функторы и т.п. Аналогия очевидная.


Источники[править]

  1. ↑ Климец А. П. "Физика и философия. Поиск истины", из-во «Форт», Брест, 1997, с.88-92
  2. ↑ Климец А. П. Постигая мироздание. Физико-философские очерки., Из-во LAP LAMBERT Academic Publishing, Германия, 2012, с.69-72
  3. ↑ Дёмин В.Н. Основной принцип материализма: Принцип материальности и его роль в научном познании. — М.: Политиздат, 1983. — 239 с. — (Над чем работают, о чем спорят философы).
  4. ↑ Архангельский А. В. Конечномерные векторные пространства, Москва, Изд-во Московского университета, 1982, с.32
  5. ↑ "Higher-Dimensional Algebra and Planck-Scale Physics", John C. Baez, 1999
Источник — http://cyclowiki.org/w/index.php?title=Пространство_(многомерная_модель)&oldid=2719688