Задача о счастливых билетах

Счастливый билет

#187. Какова вероятность счастья? (Разбираемся в математике счастливых билетов) // Wild Mathing [10:25]

Задача о счастливых билетах — условное название комбинаторной задачи подсчета количества последовательностей цифр длины 6, начиная с 000000 и до 999999, у которых сумма первых трех цифр равна сумме трех последних. Система счисления при этом предполагается десятичной, то есть цифры берутся от 0 до 9. Название задачи происходит от используемого в некоторых течениях городской культуры в СССР и России термина «счастливый билет» в отношении билетов общественного транспорта с суммой первых трех цифр равной сумме трех последних цифр или аналогичными свойствами. Задача может быть решена перебором, существуют и явные формулы ее решения. Возможное обобщение задачи — решать ее при четном числе цифр 2n и в m-ичной системе счисления (m, n — натуральные числа), то есть вычислять количество последовательностей цифр длины 2n, у которых сумма первых n цифр равняется сумме n последних цифр, а сами цифры берутся от 0 до m. Разбиралась в нескольких публикациях в журнале «Квант» в 1970-х и 1980-х годах, согласно С. К. Ландо предлагалась А. А. Кирилловым на своем семинаре в МГУ в 1970-е годы.

Явные формулы решения

Методом производящих функций в книге С. К. Ландо «Производящие функции» выводится следующая формула для числа 6-значных счастливых билетов в десятичной системе счисления.

Обозначим многочлен $A_{1}(s)=1+s+s^{2}+...+s^{9}$. Он обладает свойством, что коэффициент при $s^{n}$ равен числу однозначных чисел, сумма цифр которых равна $n$. Отсюда следует, что коэффициент при $s^{n}$ в многочлене $A_{3}(s)=(A_{1}(s))^{3}$ равен числу представлений числа $n$ в виде суммы трех цифр (принимающих значения от 0 до 9). Поэтому число счастливых 6-значных билетов в десятичной системе счисления равно сумме квадратов коэффициентов многочлена $A_{3}(s)$, что дает более простой по сравнению с полным перебором способ вычисления числа счастливых билетов.

Этот результат можно привести к явным формулам, использующим интеграл от тригонометрических функций, приписываемых в книге С. Ландо математику В. Дринфельду, который получил их будучи десятиклассником. В публикациях журнала «Квант» говорится, что формулы в виде интегралов прислали в журнал читатели.

Из предыдущего результата следует, что число счастливых билетов равно свободному члену (коэффициенту $p_{0}$ при члене $s_{0}$) многочлена Лорана $A_{3}(s)A_{3}\left({\frac {1}{s}}\right)$. Отсюда с помощью этого многочлена Лорана и примененной к нему теоремы Коши о вычетах выводится, что число счастливых билетов равно:

$p_{0}={\frac {1}{\pi }}\int \limits _{0}^{\pi }\left({\frac {\sin 10x}{\sin {x}}}\right)^{6}dx.$

Аналогично выводится общая формула для нахождения количества $2n$-значных счастливых билетов в $m$-ичной системе счисления:

$C_{2n,m}={\frac {1}{\pi }}\int \limits _{0}^{\pi }\left({\frac {\sin mx}{\sin {x}}}\right)^{2n}dx.$

Также число счастливых билетов совпадает с числом целых точек, лежащих строго внутри $2n$-мерного куба $[0,m+1]^{2n}$ на проходящей через его центр гиперплоскости, перпендикулярной главной диагонали, которое называется числом Петровского (в честь академика И. Г. Петровского).

Решение методом включения-исключения

Рассмотрим конечное множество $B$, элементы которого обладают некоторыми из свойств $c_{1},\ldots ,c_{r}$. Обозначим $N(c_{i})$ — число элементов множества $B$, обладающих свойством $c_{i}$, через $N(c_{i},c_{j})$ — число элементов множества $B$, обладающих свойствами $c_{i}$ и $c_{j}$ ($i\neq j$) и т. д. Пусть $|B|$ — общее число элементов множества $B$.

При этих обозначениях число элементов множества $B$, для которых не выполнено ни одно из свойств $c_{i}$ ($i=1,\ldots ,r$) равно (принцип включения-исключения):

$|B|-N(c_{1})-\ldots -N(c_{r})+N(c_{1},c_{2})+\ldots -N(c_{1},c_{2},c_{3})-\ldots$

Число 10-ичных шестизначных счастливых билетов равно числу билетов с суммой цифр, равной 27 (это следует из того, что каждому счастливому билету с десятичной записью $a_{1}b_{1}c_{1}a_{2}b_{2}c_{2}$ можно взаимно-однозначно сопоставить билет с десятичной записью $a_{1}b_{1}c_{1}(9-a_{2})(9-b_{2})(9-c_{2})$, который имеет сумму цифр 27. Введем множество $B$ всех расстановок неотрицательных целых чисел с суммой 27 в шести позициях, а также определим 6 свойств $c_{1},...,c_{6},$ где свойство $c_{i}$ обозначает, что число в $i$-й позиции не меньше 10. Число способов расставить $p$ неотрицательных целых чисел с суммой $q$ выражается через число сочетаний и равно $C_{p+q-1}^{p-1}$. Поэтому имеем $|B|=C_{32}^{5}$ (число способов распределить 27 в 6 позиций), $N(c_{i})=C_{22}^{5}$ (ставим в $i$-ю позицию число 10, а оставшуюся сумму 17 распределяем произвольно по 6 позициям), $N(c_{i},c_{j})=C_{12}^{5}$ (ставим в i-ю и j-ю позицию число 10, а оставшуюся сумму 7 распределяем произвольно по 6 позициям), $N(c_{i},c_{j},c_{k})=0$ (общая сумма 27 меньше, чем 30).

Таким образом, по принципу включения-исключения число 6-значных 10-ичных счастливых билетов равно

$C_{32}^{5}-6C_{22}^{5}+15C_{12}^{5}=55252.$

Аналогично выполняется общая формула для нахождения количества $2n$-значных счастливых билетов в $m$-ичной системе счисления, которое равно числу билетов с суммой цифр $n(m-1)$:

$C_{2n,m}=\sum \limits _{k=0}^{\left[{\frac {(m-1)n}{m}}\right]}(-1)^{k}C_{2n}^{k}C_{(m-1)n+2n-1-mk}^{2n-1}$

Ее также можно вывести с помощью производящих функций.

Рекуррентное соотношение

Обозначим через $N_{n}(k)$ количество $n$-значных $m$-ичных чисел ($n=1,2,3,...$), сумма цифр каждого из которых равна $k$. В частности, $N_{n}(k)=0$ при $k<0$ и $k>(m-1)n.$ Очевидно, $N_{n}(0)=1$.

Поскольку $n$-значное число с суммой цифр $k$ получается из $(n-1)$-значного числа с суммой цифр $l$ (где $k-(m-1)\leq l\leq \ldots \leq k$) путем добавления цифры $k-l$, то:

$N_{n}(k)=\sum \limits _{l=k-(m-1)}^{k}N_{n-1}(l).$

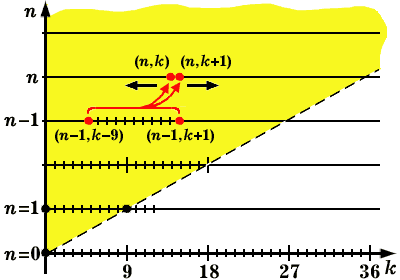
Отсюда получается рекуррентное соотношение, с помощью которого можно последовательно вычислять числа $N_{n}(k)$:

$N_{n}(k+1)-N_{n}(k)=N_{n-1}(k+1)-N_{n-1}(k-(m-1)).$

Имеем, что число счастливых $2n$-значных $m$-ичных билетов $C_{2n,m}=N_{2n}((m-1)n),$ так как оно равно числу билетов с суммой цифр $n(m-1).$

С помощью данного рекуррентного соотношения можно дать элементарное (не использующее теорию функций комплексного переменного) доказательство формулы для числа счастливых билетов в виде интеграла.

Литература

• Ландо С. К. Лекции о производящих функциях — М.: МЦНМО, 2004. ISBN 5-94057-042-9

Ссылки

• Считаем счастливые билеты. Статьи из «Кванта»