Формула Ленгмюра
Формула Ленгмюра — аналитическая зависимость электрического тока от разности потенциалов между анодом и катодом в вакууме.
Физические основы[править]
Если в вакууме расположить два электрода и создать между ними разность потенциалов, то в результате термоэлектронной или электронной эмиссии между ними может протекать электрический ток. Формула Ленгмюра применима с некоторыми изменениями и к ионному току в вакууме. В отличие от обычных проводников, в межэлектродном пространстве в вакууме создаётся поле пространственного заряда, возникающее благодаря электронам, вылетевшими из катода, а те электроны, которые покидают катод позже, этим полем тормозятся[1].
Вид формулы Ленгмюра изменяется в зависимости от геометрической формы электродов, катода и анода, а также конфигурации окружающего их пространства. Однако, суть формулы Ленгмюра состоит в том, что зависимость силы тока от приложенного напряжения пропорционально степени .
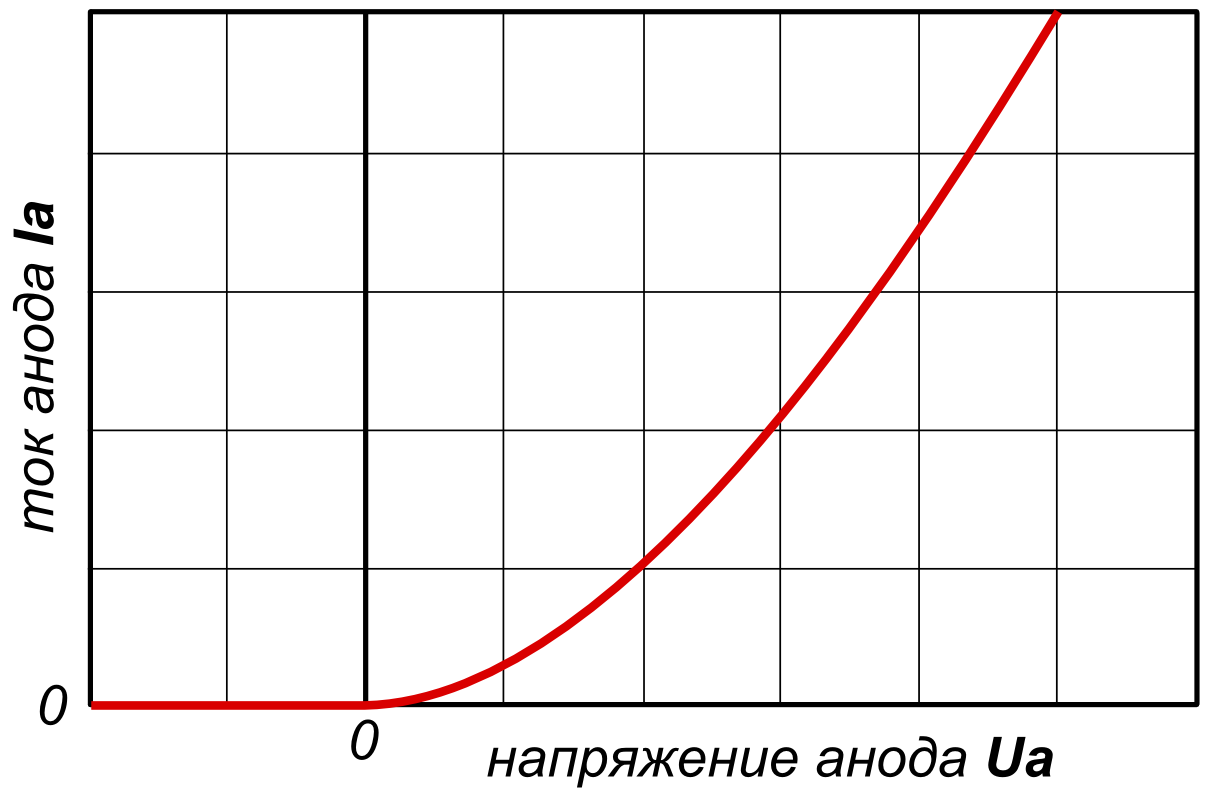
Графическая зависимость формулы Ленгмюра (закона трёх вторых) показана на рисунке 1.
В 1911 году американский физик К. Чайлд вывел аналитическую зависимость тока электронов между электродами в вакууме в предположении, что их начальная скорость вылета из катода равна нулю, а электроды представляют собой бесконечные параллельные плоскости, расположенные на расстоянии друг от друга. Формула Ленгмюра, иначе называемая законом трёх вторых, описывает зависимость силы тока от потенциала между анодом и катодом, расположенными в вакууме, с учётом пространственного заряда между этими электродами, создаваемого электронами или другими заряженными частицами. Механизм прохождения тока в вакууме и возникновение пространственного заряда объясняется тем, что в результате электронной (или ионной), термоэлектронной (или другого типа) эмиссии электроны покидают катод и направляются в сторону анода под действием электрического поля. Однако этому процессу препятствует наличие электронов между анодом и катодом, создающим собственный локальный объёмный пространственный заряд (электронное облако). Размеры и форма электронного облака зависят от конкретной конфигурации системы электродов, величины электрического потенциала между электродами и обильности эмиссии носителей заряда из катода. В простейших случаях было экспериментально установлено, что ток между катодом и анодом пропорционален приложенному напряжению в степени 3/2[2]:
, или, более точно:
,
где — заряд электрона, — масса электрона, — расстояние между катодом и анодом.
Аналитически подтверждение этому экспериментальному факту было выполнено Клементом Чайлдом в 1911 году в предположении бесконечных электродов и нулевой начальной скорости электронов, покидающих катод в результате электронной эмиссии. В 1913 году И. Ленгмюром была получена более точные формулы для разных конфигураций электродов. Так, для цилиндрических электродов было получено:
,
где была — «погонная» сила тока, то есть сила тока на единицу длины цилиндра, — радиус внешнего цилиндра (анода), а — функция отношения радиусов внешнего и внутреннего цилиндров.
Ленгмюр вывел похожую формулу для сферических электродов (сфер), введя функцию отношения радиусов внешней и внутренней сфер :
,
где — ток электронов в вакууме в случае сферических электродов (катодом выступала меньшая, внутренняя сфера).
В наиболее общем виде формула Ленгмюра может быть представлена в виде:
,
где — ток Ленгмюра, — коэффициент, зависящий от конфигурации электродов и окружающего их пространства; этот коэффициент для вакуумных диодов называют первеансом.
Границы применимости закона трёх вторых показаны на рисунке 2.
Границы применимости[править]
Формула Ленгмюра применима не во всех диапазонах приложенного напряжения и действует не для всех частот. При нулевом напряжении между электродами ток между ними отличен от нуля. Это явление называется «эффектом Эдисона». Полностью прекратить ток между электродами в реальных вакуумных диодах удаётся только при подаче отрицательного, запирающего напряжения на электрод (порядка нескольких вольт), см. рисунок 2. В области средних напряжений (т. н. режим пространственного заряда) формула Ленгмюра работает хорошо, а далее, в области насыщения тока, снова наблюдаются отклонения экспериментальных данных от следствий теоретической модели. Это связано с увеличением температуры катода и, как следствие, увеличение темпа термоэлектронной эмиссии. При переходе в режим насыщения начинает действовать эффект Шоттки, при котором работа выхода электрона уменьшается при дальнейшем увеличении напряжённости электрического поля.
Источники[править]
Литература[править]
- Храмов Ю. А. Ленгмюр Ирвинг (Langmuir Irving) // Физики : Биографический справочник / Под ред. А. И. Ахиезера. — Изд. 2-е, испр. и доп. — М. : Наука, 1983. — С. 161. — 400 с. — 200 000 экз.
- Батушев, В. А. Электронные приборы. — Москва: Высшая школа, 1969. — 608 с. — 90,000 экз.
- Дулин В. Н., Аваев Н. А., Дёмин В. П. и др. Электронные приборы / Под ред. Г. Г. Шишкина.. — Москва: Энергоатомиздат, 1989. — 496 с. — ISBN 5-283-01472-X.
- Добрецов Л. Н. Электронная и ионная эмиссия. — Москва, Л.: Гос. изд-во технико-теорет. лит., 1952. — 312 с.
- Иориш, А. Е., Кацман, Я. А., Птицын, С. В. Основы технологии производства электровакуумных приборов. — Москва, Л.: Госэнергоиздат, 1961. — 516 с. — 14,000 экз.
- Рейх, Г. Дж. Теория и применение электронных приборов. — Л.: Госэнергоиздат, 1948. — 940 с. — 7,000 экз.
- перевод с англ. Reich, Herbert J. Theory and applications of electron tubes. — 2-nd ed. — McGraw-Hill Book Company, Inc, 1944. — 716 с.
- Грановский В. Л. Электрический ток в газе. — Москва : Наука, 1971.
- Мойжес Б. Я., Пикус Г. Е. Термоэмиссионные преобразователи и низкотемпературная плазма. — Москва : Наука, 1973.
- Яшин М. С., Онуфриев В. В. Высокотемпературный термоэмиссионный преобразователь с пониженным давлением паров цезия и сверхвысокотемпературным составным коллектором // Инженерный журнал: наука и инновации. — 2020. — № 4 (100).
- Гусев Ю. П., Шёлковой Е. В. Сопротивление низковольтной электрической дуги для расчёта коротких замыканий в расширенном диапазоне токов // Вестник Ивановского государственного энергетического университета. — 2018. — № 6.
- Капцов Н. А. Коронный разряд и его применение в электрофильтрах. — Москва, Ленинград : Гостехиздат, 1947.
- Левитов В. И. Корона переменного тока. Вопросы теории, методов исследования и практических характеристик — Москва : Энергия, 1975.
- Райзер Ю. П. Физика газового разряда. — Москва : Наука, 1992.
- Соколова М. В. Коронный разряд в газах // Энциклопедия низкотемпературной плазмы. Т. 2 — Москва : Наука, 2000.
- Кечиев Л. Н., Пожидаев Е. Д. Защита электронных средств от воздействия статического электричества. — Москва : Изд. дом «Технологии», 2005.
Ссылки[править]
↑ | |
|---|---|
| Стабилитроны | |
| Коммутирующие лампы | |
| Индикаторы | |
| Разрядники | |
| Датчики | |
| Виды газового разряда | |
| Прочее | |
Одним из источников, использованных при создании данной статьи, является статья из википроекта «Рувики» («ruwiki.ru») под названием «Формула Ленгмюра», расположенная по адресу:
Материал указанной статьи полностью или частично использован в Циклопедии по лицензии CC-BY-SA 4.0 и более поздних версий. Всем участникам Рувики предлагается прочитать материал «Почему Циклопедия?». |