Метод интервалов

Метод интервалов — это метод решения рациональных неравенств вида f(x) > 0, основанный на разбиении числовой прямой на интервалы, на каждом из которых выражение сохраняет свой знак.

Решение неравенства методом интервалов

Знаки неравенства при решении неравенств методом интервалов

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. Для определения верности неравенства нужно найти его решение — значение переменной, при подстановке которого выражение становится справедливым.

Решить неравенство значит найти множество, для которых оно выполняется. При этом важно обратить внимание на знак выражения неравенства.

Обозначение при нестрогом знаке неравенства

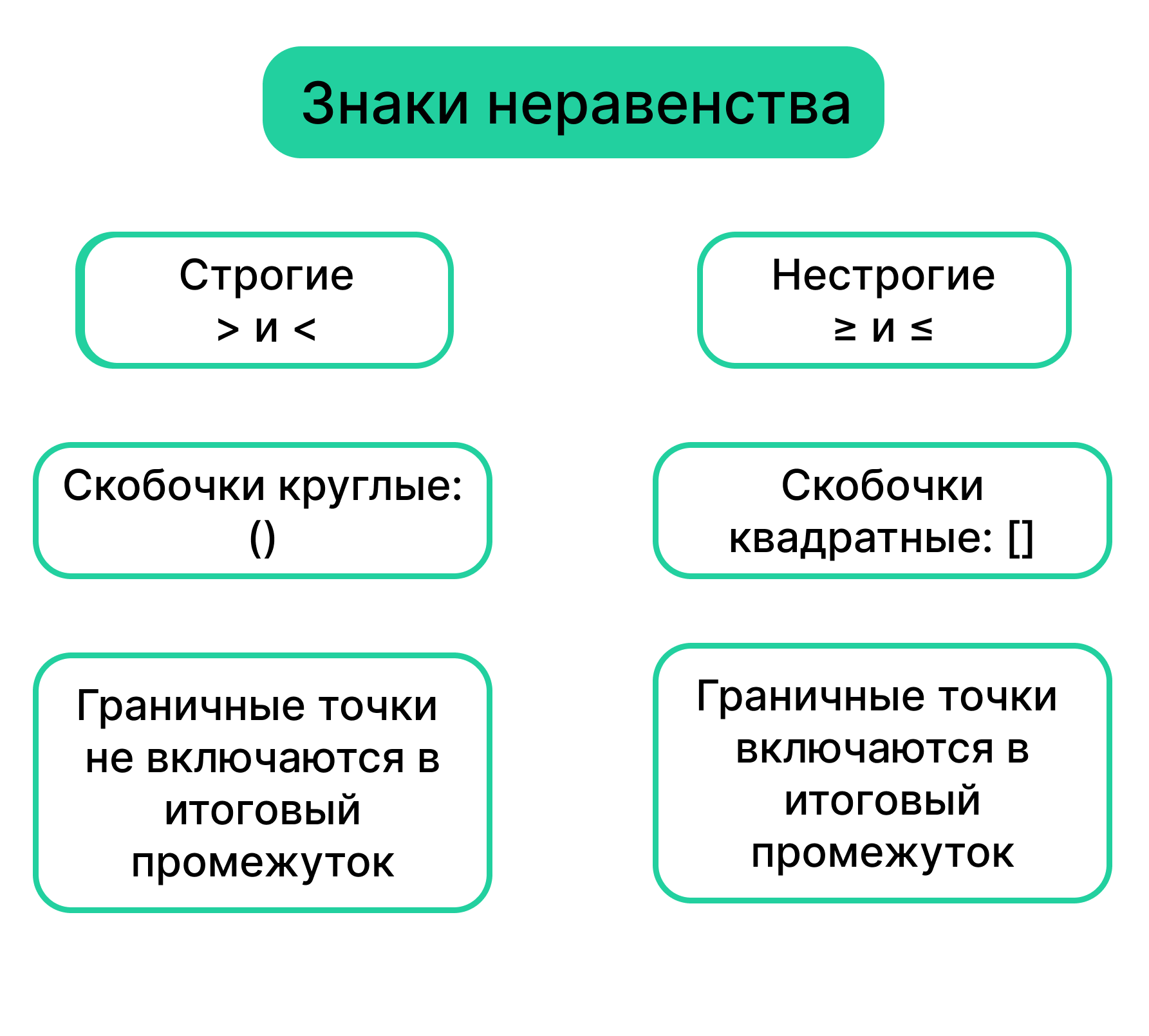
Для записи неравенств используют знаки > , < , ≥ , ≤ . При этом «>» и «<» являются строгими знаками, а «≥» и «≤» — нестрогими.

Обозначение при строгом знаке неравенства

При решении неравенств в итоговые интервалы (промежутки на числовой прямой, ограниченные двумя различными числами) включают граничные точки. При строгих знаках выражения точки включают в итоговые промежутки, при нестрогих — нет.

Алгоритм решения квадратных неравенств методом интервалов

1. Перенос всех частей неравенства в одну сторону так, чтобы с другой остался только 0.
2. Поиск нулей функции, для этого необходимо решить уравнение f(x) = 0.
3. Изображение числовой прямой с отмечанием на ней всех полученных корней. Таким образом, числовая прямая разобьётся на интервалы.
4. Определение знаков на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале. При этом знаки расставляются на оси, начиная справа.

Определение знаков при решении неравенств методом интервалов

При решение неравенств важно помнить, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.

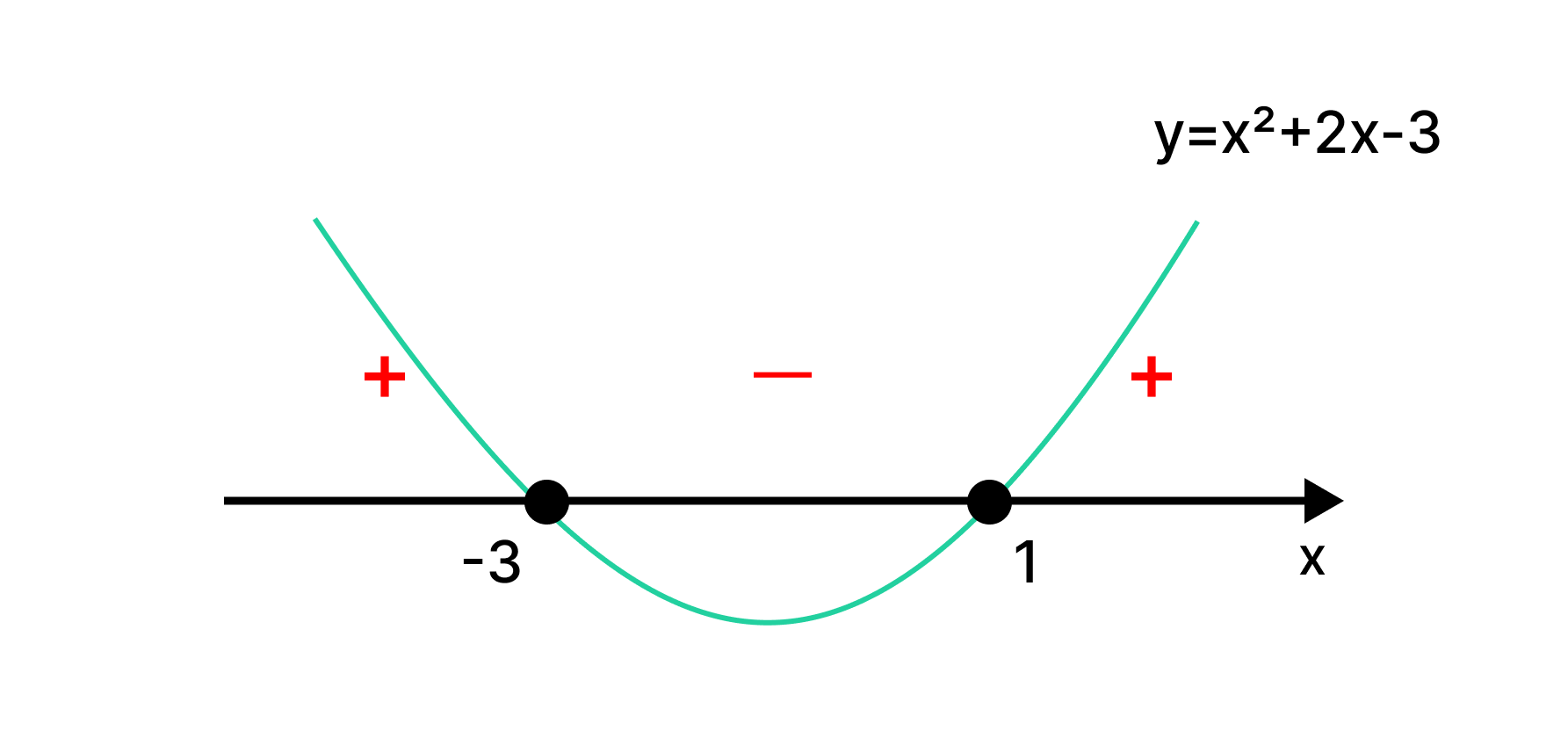
Рассмотрим функцию y=x² + 2x − 3. Её графиком служит парабола, пересекающая ось X в точках −3 и 1. Ветви параболы направлены вверх. На интервалах x < −3 и x > 1 парабола идёт выше оси X; там y > 0 и стоит знак плюс. На интервале −3 < x < 1 парабола идёт ниже оси X; там y < 0 и стоит знак минус.

Знаки функции f(x) = x² + 2x − 3

Правила чередования знаков

• Если корень неравенства повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
• Если корень неравенства повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.

Значение коэффициента а

• Если a > 0, последовательность знаков: +, −, +.
• Если a < 0, последовательность знаков: −, +, −.

См. также

• Графический метод решения
• Дискриминант
• Неравенство

Литература

• Гумеров И. С. Один из способов изучения обобщённого метода интервалов // Школьные технологии. 2017. с. 71—73.
• Ляхова Н. Е. Основные положения построения курса по выбору «Метод интервалов, метод областей и их приложения» // Вестник Таганрогского института имени А. П. Чехова. 2013.
• Абасов Р. З. Рациональный вариант метода интервалов при решении некоторых задач с модулем // Вестник Томского государственного педагогического университета. 2013. 8 (136). с. 186—191.

Ссылки

• Примеры решения неравенств методом интерваловPDF(248 КБ)

Одним из источников, использованных при создании данной статьи, является статья из википроекта «Рувики» («ruwiki.ru») под названием «Метод интервалов», расположенная по адресу: — «https://ru.ruwiki.ru/wiki/Метод_интервалов» Материал указанной статьи полностью или частично использован в Циклопедии по лицензии CC-BY-SA 4.0 и более поздних версий. Всем участникам Рувики предлагается прочитать материал «Почему Циклопедия?».