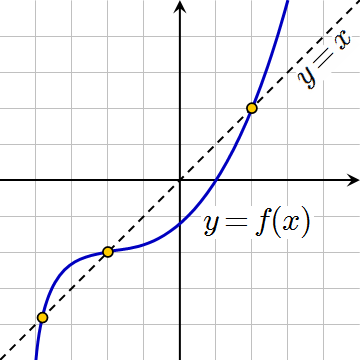
Уравнение

Иллюстрация графического метода нахождения корней уравнения x = f(x)

Что такое уравнение // Денис Большаков [4:29]

Уравнение, которое меняет взгляд на мир [Veritasium] // Vert Dider (1 февр. 2020 г.) [17:24]

Уравнение — аналитическая запись задачи нахождения аргументов, при которых две заданные функции равны между собой.

$f(x)=g(x)\,$,

где $f(x)\,$ и $g(x)\,$  — некоторые заданные функции, которые называются левой и правой частями уравнения, x  — элемент множества, на которой определены функции f и g.

Аргументы функций уравнения называют неизвестными (величинами), значения неизвестных, при которых уравнения становится равенством — корнями уравнения. Уравнение может иметь один, несколько или бесконечно много корней, а может не иметь корня вообще.

Иногда математическая задача накладывает ограничения на множество, которому должны принадлежать решения уравнения, например, диофантово уравнение требуют только целочисленного решения. Существование и количество корней уравнения тоже могут зависеть от множества: например, уравнение $x^{2}=-1$ не имеет действительных решений, но имеет комплексные решения.

Нормальная форма записи уравнения имеет вид: $F(x)=0$.

К нему можно перейти, перенеся правую часть уравнения налево. Уравнение в такой форме называется однородным.

Для того, чтобы решить уравнение, надо найти его решения или доказать, что их не существует.

Аргументами функции, а, следовательно, неизвестными уравнения могут быть не только числа, но и более сложные математические объекты. Например, в дифференциальных уравнениях неизвестными являются функции, в операторных — операторы и т. д.

Эквивалентность уравнений

Два уравнения называются эквивалентными или равносильными, если каждый корень одного уравнения является корнем второго уравнения и наоборот.

Эквивалентность уравнений имеет свойство рефлексивности: если одно уравнение эквивалентно второму, то второе уравнение эквивалентно первому.

Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно второму, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения.

Третье важное свойство задается теоремой: уравнение

$f_{1}(x)\cdot f_{2}(x)=0\,$

эквивалентно совокупности уравнений:

$f_{1}(x)=0,\qquad f_{2}(x)=0.\,$

Это означает, что все корни первого уравнения являются корнями одного из двух других уравнений, и позволяет находить корни частями.

Следствие уравнения и посторонние корни

Уравнение

$F(x)=G(x)\,$

называется следствием уравнения

$f(x)=g(x)\,$,

если все корни второго уравнения являются корнями первого. В общем первое уравнение может иметь дополнительные корни, которые по второму уравнению называются посторонними. Посторонние корни могут появиться при преобразованиях, необходимых для нахождения корней уравнений. Для того, чтобы их обнаружить, нужно проверить корень подстановкой в исходное уравнение. Если при подстановке уравнение становится тождеством, то корень настоящий, если нет — посторонний.

Основные свойства уравнений

С алгебраическими выражениями, входящими в уравнения можно выполнять операции, которые не изменяют его корней, в частности.

1. В любой части уравнения можно раскрыть скобки.
2. В любой части уравнения можно свести подобные слагаемые.
3. Любой член уравнения можно перенести из одной части в другую, заменив его знак на противоположный.
4. Обе части уравнения можно умножать или разделить на одно и то же число, отличное от нуля.

Уравнения, которые являются результатом этих операций являются эквивалентными начальному уравнению.

Возведение обеих частей уравнения в квадрат может привести к появлению посторонних корней.

Решения уравнений

Отдельные классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, но и позволяют записать решение в виде формулы, в которую могут входить параметры. Такие аналитические выражения позволяют не только вычислить корни, но и провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней.

К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвертой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвертой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней.

Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны.

В общем случае, когда аналитического решения найти не удается, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определенного заранее заданного значения.

Применение

Уравнения часто возникают при решении практических или теоретических задач в различных областях науки и техники: физике, химии, экономике и т. д.

Уравнения и формулы

Математические уравнения достаточно изученный объект и существуют как аналитические, так и численные методы их решения. Благодаря этому задачи других областей сначала формулируются в виде уравнений. Для этого прежде всего нужно ввести обозначения неизвестных величин и параметров и использовать формулы соответствующих областей знаний, для того, чтобы записать соотношение между ними.

Отличие от формулы и уравнения в том, что формула является правилом для вычисления какой величины и обычно имеет форму:

$y=f(x_{1},x_{2},\ldots ,x_{n})\,$,

где у — величина, которую надо вычислить, а $f(x_{1},x_{2},\ldots ,x_{n})$ определенная функция из набора параметров. При применении формулы нужно подставить в нее значения параметров и получить значение y. Однако, каждую формулу можно трактовать также как уравнение, если известно значение y, и нужно найти значения параметров, при которых оно реализуется. В этом случае параметры, или часть параметров, становятся неизвестными.

Особенности уравнений в физике

Особенностью уравнений в физике является то, что переменные, которые обозначают физические величины, являются обычно размерными. Размерность позволяет проводить дополнительную проверку вычислений, поскольку размерность результата должна быть правильная. Если величины и параметры, заданны в задаче в разных единицах, все единицы перед решением уравнения должны быть сведены к одной системе единиц. Для численного решения физических задач, физическое уравнение нужно сначала обезразмерить, то есть ввести новые безразмерные переменные. Такие переменные обычно получают, деля определенную физическую величину на ее характерное значение.

Некоторые из уравнений физики имеют свои собственные названия, например, уравнение движения описывает эволюцию физической системы, а уравнение состояния в термодинамике задаёт связь между термодинамическими параметрами.

Особенности уравнений в химии

В химии химические уравнения описывают превращения веществ при химической реакции. В то же время, они могут использоваться для определения баланса веществ при таких реакциях, то есть математическими уравнениями, обычно линейными.

Список уравнений

• линейное уравнение;
• квадратное уравнение;
• уравнение квадрата;
• кубическое уравнение;
• уравнение куба;
• уравнение синуса;
• уравнение косинуса;
• уравнение тангенса;
• уравнение котангенса;
• уравнение секанса;
• уравнение косеканса.

См. также

• Алгебраическое уравнение
• Уравнение теплового баланса

Литература

• Бекаревич А. Б. Уравнения в школьном курсе математики. — Минск: Нар. асвета, 1968. — 152 с.
• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Переиздание: Изд. АСТ, 2003, ISBN 5-17-009554-6.