Число
Число — понятие, связанное с математическими объектами, используемыми для счёта, измерения и обозначения.
То или иное число — например, «единица», «сотня», «треть», «ноль», 359, «фи», «число Эйлера», «мнимая единица i», «гугол» и так далее без конца — термин, самостоятельно, лишь наличием своего знака, определяющий некоторую меру: меру счётного количества, величины́, угла, отступа, объёма. Некоторые рода́ чисел способны выражать сопряжённую систему мер: комплексное число, пропорция, вектор, кватернион. Чи́сла часто упоминаются при характеристике предмета математики, и довольно общепринято число мнить, как основное[1] понятие в классической математике.
Общая информация[править]
«Число неких единиц» — произвольных сущностей или явлений — в общем случае указывает меру их счётного количества в данном множестве или классе: «две стороны́», «три угла», «восемь бит», «38 снайперов». Такой повседневный смысл соответствует понятию натурального числа́, центральному в Теории чисел. Натуральные чи́сла обобщаются расширением области значений до целых, рациональных, вещественных, комплексных, кватернионов, векторов и так далее.
В языке натуральные числа представлены числительными. Отдельные натуральные числа могут выражаться через последовательность символов, знаков, называемых цифрами; например, «5» — это цифра, обозначающая число пять. Покуда можно запомнить только небольшое количество символов, основные чи́сла обычно организованы в некоторую систему счисления: та представляет собой организованный способ представления, репрезентации некоего числа́. Наиболее распространенная система счисления — десятичная система счисления, где любое число выражается комбинацией из десяти цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).[2]
Чи́сла также разделяются на порядковые и кардинальные: разница проявляется в классификации бесконечных множеств, которые могут быть или не быть счётными. В частности, континуум строго несчётный и равен по «размеру» — множеству всех подмножеств натуральных чисел: , где ℵ0 — первичное кардинальное трансфинитное число, мощность множества натуральных чисел .
Изначально под числами подразумевались только натуральные числа: 1, 2, 3, 4, и так далее[3]. В античной науке только натуральное число называлось собственно числом, ἀριθμός. В дальнейшем, понятие о числе было расширено, и числами стали называть многие прочие математические объекты, среди которых вещественные числа, комплексные числа, кватернионы и элементы разных числоподобных координатных систем. Отношение произвольных длин в классическом греческом называлось λόγος. «Иррациональное» — латинская калька для численно невыразимой пропорции, ἄλόγος. Логарифм придуман Джоном Непером, как стяжение двух ранее различаемых терминов.
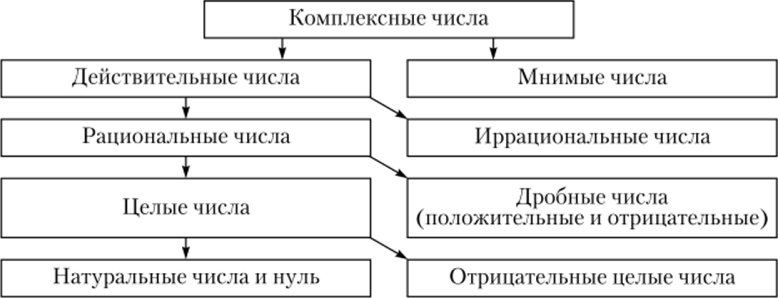
Классификация[править]
Это числа, которые используются при счете: 1, 2, 3… и т. д.
Ноль не является натуральным.
Натуральные числа принято обозначать символом N.
- Целые числа. Положительные и отрицательные числа
Два числа отличающиеся друг от друга только знаком, называются противоположными, например, +1 и −1, +5 и −5. Знак «+» обычно не пишут, но предполагают, что перед числом стоит «+». Такие числа называются положительными. Числа, перед которыми стоит знак «−», называются отрицательными.
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Это конечные дроби и бесконечные периодические дроби. Например,
Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Бесконечная непериодическая дробь называется иррациональным числом. Например:
Множество иррациональных чисел обозначается J.
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.[4]
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен −1, то есть i² = −1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi.[5]
Применение[править]
Числа имеют применение:
- в арифметике — «азбуке» числовых построений
- для задания/указания величин:
- в приближениях к другим величинам или мерам °C
- в кодах, несущих информацию 31337
- для хранения промежуточных данных в ходе вычислений #880088
- в качестве номеров во всевозможных обозначениях:
- в указателях (индексах) и иных номерных списках
- в последовательностях и иных системах отсчёта: «третий с конца», «2012 год», «Второе пришествие Христа»
- в произвольных нумерациях: «359-й автобус»
- как элементы класса — чи́сла некоего свойства:
- в выражениях составного формализма:
- в алгебраических полях
- в системах аналитических координат
- в системе географических координат 47°9′S 126°43′W
- в векторных пространствах
- в матрицах…
- (ad infinitum)
Всевозможные числа могут быть упомянуты вне практического контекста. Мощь математического языка позволяет создавать произвольные числовые математические объекты и обобщения концепции чисел, служащих образовательным, исследовательским или даже развлекательным мотивам, и, так или иначе, несущим образцы математической красоты: например, магические квадраты, поля судоку, последовательности Лэнгфорда, сюрреальные числа, и́гры…
Расширение понятия числа[править]
Появление дробных чисел[править]
При вычислении длины (или другой единицы: объёма, массы и т.д.) с использованием «эталонной» меры результат измерения не всегда укладывался в целое количество — для этого были введены дробные числа. Жители Древнего Египта использовали аликвотные дроби, то есть дроби, числитель которых всегда равен 1, а знаменатель — натуральное число. Вавилоняне выражали дробные числа в традиционной для них шестидесятиричной системе. Индийцы и китайцы на заре н. э. пользовались уже привычными для современного человека обыкновенными дробями и могли выполнять все арифметические действия с ними.
В начале XV века благодаря персидскому учёному Аль-Каши были введны и стали широко применяться десятичные дроби. В Европе же они начали распространяться после выхода книги фламандского математика Симона Стевина «Десятая» (нидерл. De Thiende), вышедшей в 1585 году.
Появление отрицательных чисел[править]
Последующее расширение понятия числа уже не было связано с непосредственным счётом. С развитием алгебры возникла необходимость введения отрицательных чисел — без них ряд задач были нерешаемы. И если в Индии отрицательными числами пользовались уже с VI века, то в Европе они укоренились лишь во времена Декарта (XVII век), при помощи аналитической геометрии показавшего, что корни уравнения можно рассматривать как координаты точек пересечения линии с осью координат. Целые и дробные числа (положительные и отрицательные), а также нуль, получили название рациональных чисел.
Ещё учёными Древней Греции было замечено, что не все отрезки можно выразить целым или дробным числом. В частности, Евклид в «Началах» отмечал, что длина диагонали квадрата с точно заданными длинами сторон не является рациональным числом.
См. также[править]
Источники[править]
- ↑ wikt:ru:число
- ↑ «numeral, adj. and n.». OED Online (Oxford University Press).
- ↑ «number, n.» (en-GB). OED Online (Oxford University Press).
- ↑ http://fizmat.by/math/arithmetic/numeric
- ↑ https://elementy.ru/posters/fractals/complex_numbers
Числовые системы ↑ | |
|---|---|
множества |
Натуральные числа () • Целые () • Рациональные () • Алгебраические () • Периоды • Вычислимые |
и их расширения |
Действительные (вещественные) () • Комплексные () • Кватернионы () • Числа Кэли (октавы, октонионы) () • Седенионы () • Альтернионы • Дуальные • Гиперкомплексные • Супердействительные • Гипервещественные |
числовые системы |
Кардинальные числа • Порядковые (трансфинитные, ординалы) • p-адические • Сверхнатуральные • Сюрреальные |
|
Двойные • Иррациональные • Трансцендентные • Числовой луч • Положительные числа • Простые числа • Бикватернионы • Координатизация • Расширение понятия числа | |