Смысл дифференциалов

Основная статья — дифференциал (математика)

Смысл дифференциалов — объяснение того, как можно охватить весь «смысл дифференциалов» и почему они играют большую роль в математическом анализе.

Геометрический смысл

Дифференциал как инфинитезималь

Как указывалось в основной статье, последователи Лейбница и Лопиталя воспринимали дифференциал как бесконечно малое число. В частности, дифференциал независимой переменной понимали как бесконечно малую длину элементарного отрезка оси Ox, который, по их представлениям, был более неделим.

Дифференциал в современном понимании

Традиционно в современных источниках при ознакомлении с дифференциалами приводится геометрический смысл производной, основанном на касательной. Дифференциалом функции y = f(x) называется то (dy), насколько изменится ордината точки при её перемещении по касательной, если сдвиг этой точки по абсциссе будет равен dx. Таким образом, вектор {dx, dy} будет пониматься как направляющий вектор этой касательной.

Файл:Sentido geometrico del diferencial de una funcion.png

Дифференциальные уравнения

Исторически оказалось, что дифференциалы имеют огромный вес в решении дифференциальных уравнений.

Пример — радиоактивный распад

Файл:Radioactive decay-ru.svg

Угловой коэффициент касательной прямо пропорционален самой ординате точки касания

Известно, что скорость, с которой количество радиоактивного вещества N уменьшается в течение времени t, оказывается прямо пропорциональна N. Такое утверждение можно записать как:

$N'(t)=aN(t),$

где a — отрицательная константа. Ниже будут показаны два способа решения этого уравнения относительно N(t).

Метод приращений. Решить данное уравнение можно, раскрыв определение производной:

$\lim _{\Delta t\to 0}{\frac {\Delta N}{\Delta t}}=aN(t)\Longleftrightarrow {\frac {\Delta N}{\Delta t}}=aN+\epsilon (t,\Delta t),$

где ε — функция такая, что

$\lim _{\Delta t\to 0}\epsilon (t,\Delta t)=0.$

Тогда можно в одну часть равенства «занести» всё, что связано с N, а в другую — с t.

$\Delta N=aN\Delta t+\epsilon (t,\Delta t)\Delta t\Longleftrightarrow {\frac {\Delta N}{N}}+\epsilon _{2}(t,\Delta t)\Delta t=a\Delta t.$

А далее, чтобы «избавиться» от дельт, нужно произвести суммирование приращений, начиная с некоторого начального отсчёта t₀:

$\sum _{u=t_{0}}^{t}({\frac {\Delta N(u)}{N(u)}}+\epsilon _{2}(u,\Delta u)\Delta u)=a\sum _{u=t_{0}}^{t}\Delta u.$

Тогда заметим, что ΔN/N с точностью до некоторой погрешности вида ε Δt равняется Δ ln N, где ln — log_e. Далее, «избавиться» от всех эписилонов можно, если суммирование проводить по бесконечно малому шагу Δu:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lim_{\Delta u\to0}\sum_{u=t_0}^t(\Delta\ln N(u) + \epsilon_3(u,\Delta u)\Delta u) = a(t - t_0) \Longleftrightarrow \ln N(t) - \ln N(t_0) = a(t - t_0) \Longleftrightarrow N(t) = N(t_0)e^{a(t-t_0)},}

где N(t₀) — начальное количество в начальный момент t₀. Именно так наглядно можно обосновать, по какому принципу происходит решение дифференциальных уравнений.

Метод дифференциалов. Для дифференциальных уравнений существует и такой мощный инструмент, как дифференциалы. Отличается такой способ тем, что в целом он даёт меньше наглядности, но позволяет больше «экономить» на эпсилонах. Однако на самом деле между методами приращений и дифференциалов имеются существенные параллели. Иначе говоря, оба метода в сущности представляют собой принципиально одно и то же.

Исходное уравнение можно переписать в следующем виде:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{dN(t)}{dt} = aN(t) \Longleftrightarrow \frac{dN(t)}{N(t)} = a\,dt.}

Тогда дифференциальную форму dN/N можно преобразовать как d ln N:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle d\ln N(t) = a\,dt.}

Далее, можно избавиться от знаков дифференциала, взяв первообразные с одинаковым начальным моментом t₀:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \int_{u=t_0}^td\ln N(u) = a\int_{t_0}^tdu \Longleftrightarrow \ln N(t) - \ln N(t_0) = a(t - t_0) \Longleftrightarrow N(t) = N(t_0)e^{a(t-t_0)}.}

Пример — гармонические колебания

В некоторых источниках понятию гармонических колебаний даётся одно из равносильных определений, в котором гармоническим колебанием по оси Ox вокруг начала координат называется колебание, при котором отклонение x прямо пропорциально ускорению a_x и противоположно ему по знаку. То есть имеется уравнение

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ddot x = -\omega^2x,}

где ω, как будет показано, — циклическая частота.

Через приращения. Для решения уравнения можно переписать как

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac1{\Delta t}\Delta\dot x = -\omega^2x + \epsilon(t,\Delta t),}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{\Delta x}{\Delta t}\Delta\dot x = -\omega^2x\Delta x + \epsilon(t,\Delta t)\Delta x \quad \Longleftrightarrow \quad (\dot x + \epsilon_2(t,\Delta t))\Delta\dot x = -\omega^2x\Delta x + \epsilon(t,\Delta t)\Delta x \quad \Longleftrightarrow \quad \dot x\Delta\dot x + \epsilon_2(t,\Delta t)\Delta\dot x = -\omega^2x\Delta x + \epsilon(t,\Delta t)\Delta x \quad \Longleftrightarrow \quad \Delta(\frac12\dot x^2) + \epsilon_4(t,\Delta t)\Delta\dot x = -\omega^2\Delta(\frac12x^2) + \epsilon_3(t,\Delta t)\Delta x.}

В ходе суммирования обеих частей последнего равенства с бесконечно малым шагом получаем уравнение в производных первого порядка:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac12(\dot x^2 - v_{0x}^2) = -\omega^2\frac12(x^2 - x_0^2),}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot x = \pm\sqrt{v_{0x}^2 + \omega^2x_0^2 - \omega^2x^2}.}

Заменим выражение Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \textstyle{\frac{\sqrt{v_{0x}^2 + \omega^2x_0^2}}\omega}} на A:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{\Delta x}{\Delta t} + \epsilon_5(t,\Delta t) = \pm\omega\sqrt{A^2 - x^2},}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{\Delta x}{\pm\sqrt{A^2 - x^2}} + \frac{\epsilon_5(t,\Delta t) \Delta t}{\pm\sqrt{A^2 - x^2}} = \omega\Delta t,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lim_{\Delta y\to0}\sum_{y=x_0}^x\frac{\Delta y}{\pm\sqrt{A^2 - y^2}} = \omega(t - t_0).}

Возьмём данную сумму относительно y/A:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lim_{\Delta y\to0}\sum_{y=x_0}^x\frac{\Delta(y/A)}{\pm\sqrt{1 - (y/A)^2}} = \omega(t - t_0)}

чтобы применить табличную первообразную:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \pm(\arccos\frac xA - \arccos\frac{x_0}A) = \omega(t - t_0),}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \pm\arccos\frac xA = \omega(t - t_0) \pm \arccos\frac{x_0}A,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x = A\cos(\omega t - \phi_0),}

где φ₀ = ωt₀ ± arccos(x₀/A).

Сравнительная таблица:

Приращения	Дифференциалы
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac1{\Delta t}\Delta\dot x = -\omega^2x + \epsilon(t,\Delta t)}	Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac1{dt}d\dot x = -\omega^2x}
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{\Delta x}{\Delta t}\Delta\dot x = -\omega^2x\Delta x + \epsilon(t,\Delta t)\Delta x}	Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{dx}{dt}d\dot x = -\omega^2x\,dx}
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (\dot x + \epsilon_2(t,\Delta t))\Delta\dot x = -\omega^2x\Delta x + \epsilon(t,\Delta t)\Delta x}	Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot x\,d\dot x = -\omega^2x\,dx}
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Delta(\frac12\dot x^2) + \epsilon_4(t,\Delta t)\Delta\dot x = -\omega^2\Delta(\frac12x^2) + \epsilon_3(t,\Delta t)\Delta x}	Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle d(\frac12\dot x^2) = -\omega^2d(\frac12x^2)}
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{\Delta x}{\Delta t} + \epsilon_5(t,\Delta t) = \pm\omega\sqrt{A^2 - x^2}}	Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{dx}{dt} = \pm\omega\sqrt{A^2 - x^2}}
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lim_{\Delta y\to0}\sum_{y=x_0}^x\frac{\Delta(y/A)}{\pm\sqrt{1 - (y/A)^2}} = \omega(t - t_0)}	Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \int_{y=x_0}^x\frac{d(y/A)}{\pm\sqrt{1 - (y/A)^2}} = \omega(t - t_0)}

Пример — интегральные линии

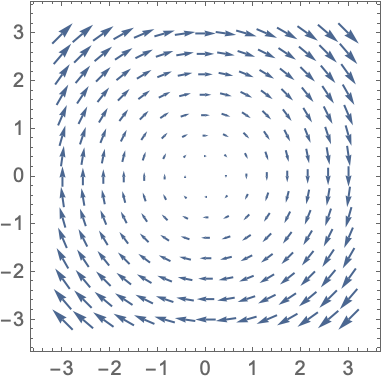
Векторное поле {y, -x} вырисовывает концентрированные окружности

Дано векторное поле. Тогда интегральной линией данного поля называется кривая, к которой это поле направлено по касательной. Рассмотрим в качестве примера функцию F(x, y) = {y, −x}. Тогда по геометрическому смыслу дифференциала вектор {dx, dy} коллинеарен {y, −x} и мы получаем уравнение интегральных линий

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y' = \frac{-x}y.}

Если точнее, то более справедливо будет раскрыть как

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle yy' = -x,}

чтобы предупредить случай, когда y' стремится к бесконечности из-за y в знаменателе. Тогда:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{y\Delta y}{\Delta x} + \epsilon(x,\Delta x) = -x}	Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{y\,dy}{dx} = -x}
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y\Delta y + \epsilon(x,\Delta x)\Delta x = -x\Delta x}	Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y\,dy = -x\,dx}
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Delta(\frac12y^2) + \epsilon_1(x,\Delta x)\Delta x = \Delta(-\frac12x^2) + \epsilon_2(x,\Delta x)\Delta x}	Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle d(\frac12y^2) = d(-\frac12x^2)}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac12(y^2 - y_0^2) = -\frac12(x^2 - x_0^2)}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x^2 + y^2 = x_0^2 + y_0^2}

И в данном примере присутствует тонкий момент: если бы мы через приращения считали изначальное уравнение, то получилось бы

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{\Delta y}{\Delta x} + \epsilon_3(x,\Delta x) = \frac{-x}y.}

Но из-за того, что есть риск, что y' обратится в бесконечность, между ε, ε₁, ε₂ с одной стороны и ε₃ с другой — возникает существенная разница:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lim_{\Delta x\to0}\epsilon = \lim_{\Delta x\to0}\epsilon_1 = \lim_{\Delta x\to0}\epsilon_2 = 0 \neq \lim_{\Delta x\to0}\epsilon_3}

при y = 0. Что любопытно, для интегральных линий данного поля число ε₃ при y = 0 не просто не стремится к 0, а, даже наоборот, отправляется к бесконечности (!).

См.также

• Инфинитезималь