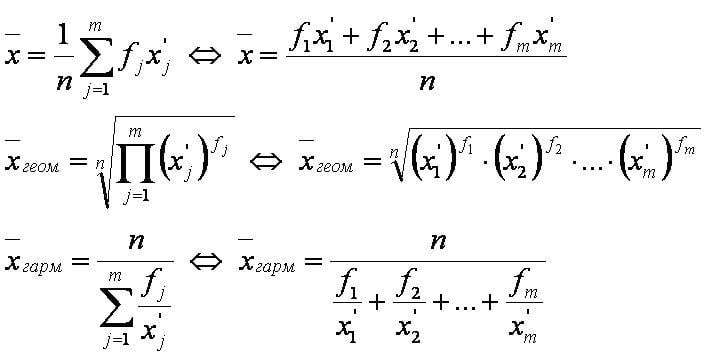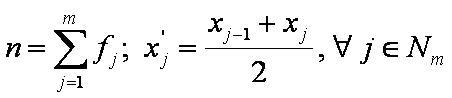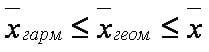Средние интервального ряда

Средняя — это числовая характеристика случайной величины, равная среднему ожидаемому значению и находящаяся между наименьшим и наибольшим значениями интервального ряда.

Виды средних:

• средняя арифметическая;
• средняя геометрическая;
• средняя гармоническая.

Обозначения:

n — объём совокупности;

m — число интервалов;

x_i-1 — нижняя граница i-ого интервала;

x_i — верхняя граница i-ого интервала;

x^’_i — середина i-ого интервала;

f_i — частота i-ого интервала;

${\bar {x}}$ — средняя — математическое ожидание.

Формулы:

где

Для средних верно неравенство:

Другие формулы:

• средние;
• дисперсия;
• среднеквадратическое отклонение;
• среднее линейное отклонение;
• мода;
• медиана;
• квартиль;
• дециль;
• начальный момент k-ого порядка;
• центральный момент k-ого порядка;
• коэффициент асимметрии;
• коэффициент эксцесса.

Ссылки

• Участник:Logic-samara