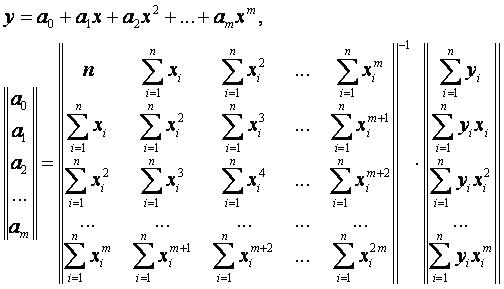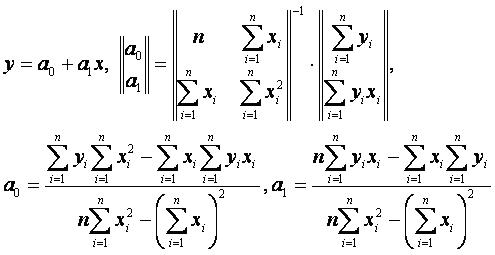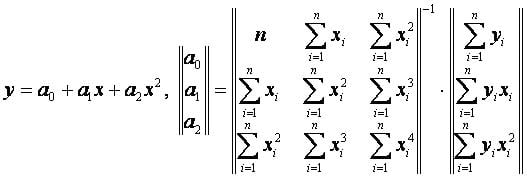Аппроксимация

Аппроксимация — это способ нахождения функции, которая наиболее соответствует таблице значений. При аппроксимации выбирается вид функции и определяются параметры этой функции, таким образом, что значения аппроксимирующей функции наиболее приближены к табличным значениям. С помощью аппроксимирующих функций возможно вычисление значений функции в точках отличных от табличных.

Описание

Суть аппроксимации методом наименьших квадратов (МНК) состоит в определении функции, имеющей наименьшую сумму квадратов отклонений аппроксимирующих значений от табличных.

Формула аппроксимации каноническим многочленом

Примеры формулы

Линейная аппроксимация (m=1)

Квадратическая аппроксимация (m=2)

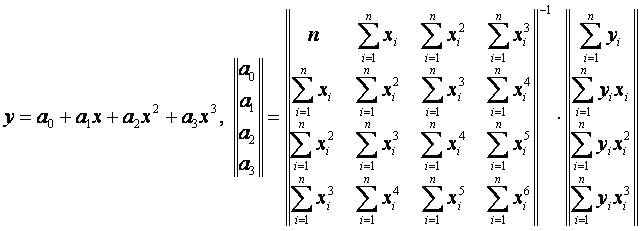
Кубическая аппроксимация (m=3)

• Заметим, что аппроксимирующая функция наиболее приближена к заданным точкам (но может не проходить через эти точки), а интерполирующая функция обязательно проходит через заданные точки.

Численные методы:

• решение уравнений;
• решение систем уравнений;
• ортогонализация;
• решение дифференциальных уравнений;
• аппроксимация;
• интерполяция;
• численное интегрирование;
• нахождение экстремумов.

Литература

• Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Наука, 1970

Ссылки

• Участник:Logic-samara