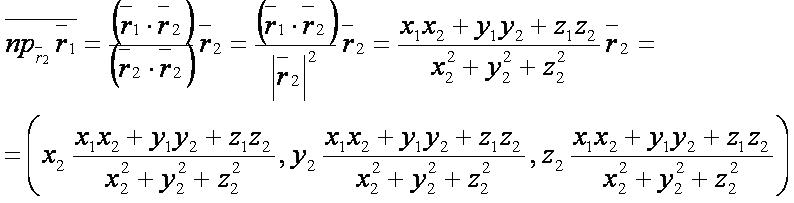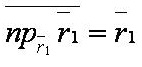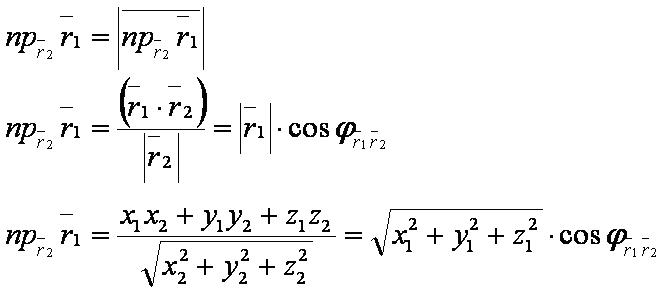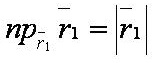Проекция вектора на вектор в трёхмерном пространстве
(перенаправлено с «Проекция вектора на вектор»)
Перейти к навигации
Перейти к поиску
Числовая проекция вектора на другой вектор (в алгебраическом смысле) — это число, равное отношению скалярного произведения этих векторов к длине второго вектора.
Векторная проекция вектора на другой вектор (в геометрическом смысле) — это вектор с длиной, равной отношению скалярного произведения этих векторов к длине второго вектора, и с направлением второго вектора.
Обозначения[править]
- — первый вектор;
- — второй вектор.
Проекции[править]
Векторная проекция[править]
Числовая проекция[править]
Другие проекции:[править]
Литература[править]
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970.