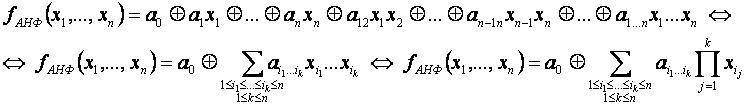Алгебраическая нормальная форма
Алгебраическая нормальная форма (АНФ) для логической функции — это упрощённый полином Жегалкина, построенный для данной функции.
При этом таблицы истинности для логической функции и её АНФ совпадают.
Обозначения[править]
n — число аргументов функции;
(x1, x2, …, xn) — набор аргументов функции;
f(x1 ,x2, …, xn) — логическая функция;
fАНФ(x1, x2, …, xn) — АНФ логической функции.
Формула[править]
- Заметим, что коэффициенты ai1…ik принимают значения из множества {0; 1}, причём если коэффициент равен нулю, то соответствующее слагаемое должно быть опущено.
Методы построения АНФ[править]
- метод эквивалентных преобразований;
- метод неопределённых коэффициентов.
Метод эквивалентных преобразований[править]
Метод использует для преобразования СДНФ логической функции. Для этого операция отрицания переменной в СДНФ заменяется на сумму по модулю два константы 1 и переменной. Операция элементарной конъюнкции сохраняется в виде произведения. Операция дизъюнкции заменяется на сложение по модулю два, так как в СДНФ при любых значениях входных переменных в единицу обращается не более одного дизъюнкта, то есть операция дизъюнкции эквивалентна операции разделительной дизъюнкции (сложению по модулю два). После этого проводятся необходимые упрощения: раскрываются скобки и сокращаются чётные повторения.
Метод неопределённых коэффициентов[править]
Метод использует таблицу истинности логической функции. Для этого берётся общий вид полинома Жегалкина, в него подставляются наборы аргументов и приравниваются к соответствующим значениям логической функции из таблицы истинности. Полученную систему уравнений упрощают и решают относительно коэффициентов. Нулевые коэффициенты опускают, а для единичных коэффициентов выписывают АНФ логической функции.