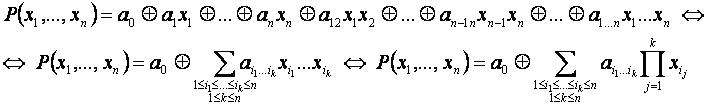Полином Жегалкина
Полином Жегалкина (многочлен Жегалкина) — это логическая функция, использующая две операции: конъюнкцию и разделительную дизъюнкцию. Полином предложен российским математиком Иваном Ивановичем Жегалкиным в 1927 году.
Назначение полинома Жегалкина — это алгебраическое выражение логических функций.
Обозначения[править]
Введём обозначения:
n – число аргументов функции;
(x1,x2,…,xn) – набор аргументов функции;
P(x1,x2,…,xn) – полином Жегалкина.
Операции:[править]
- конъюнкция;
- разделительная дизъюнкция.
Конъюнкция — это логическая операция аналогичная арифметическому произведению. Для констант используется обозначение точкой, а для переменных точка опускается.
- 0 · 0 = 0
- 0 · 1 = 0
- 1 · 0 = 0
- 1 · 1 = 1
Разделительная дизъюнкция — это логическая операция аналогичная арифметическому сложению по модулю 2. Используется обозначение знаком плюс в кружке.
- 0 ⊕ 0 = 0
- 0 ⊕ 1 = 1
- 1 ⊕ 0 = 1
- 1 ⊕ 1 = 0
Формула[править]
Полином Жегалкина имеет следующий вид:
- Заметим, что коэффициенты ai1...ik принимают значения из множества {0,1}, причём если коэффициент равен нулю, то соответствующее слагаемое может быть опущено.
- Полином Жегалкина, состоящий только из слагаемых с единичными коэффициентами (т. е. с опущенными слагаемыми с нулевыми коэффициентами), называется алгебраической нормальной формой (АНФ) соответствующей логической функции.
Примеры полиномов:[править]
С одной переменной[править]
- P(x1) = 0 — константа 0
- P(x1) = 1 — константа 1
- P(x1) = x1 — тождественность
- P(x1) = 1 ⊕ x1 — отрицание x̄1
С двумя переменными[править]
- Значения полиномов Жегалкина задаются с помощью таблицы истинности или определяются по формулам.
- Полином Жегалкина является предикатом, определённым на множестве {0,1}.
Другие понятия[править]
- отрицание;
- дизъюнкция;
- конъюнкция;
- разделительная дизъюнкция;
- импликация;
- обратная импликация;
- эквиваленция;
- стрелка Пирса;
- штрих Шеффера;
- полином Жегалкина;
- Нормальные формы:
- совершенная дизъюнктивная нормальная форма;
- совершенная конъюнктивная нормальная форма;
- минимальная дизъюнктивная нормальная форма;
- минимальная конъюнктивная нормальная форма;
- алгебраическая нормальная форма;