Минимальная дизъюнктивная нормальная форма

Минимизация функций. Карты Карно. Цифровая техника // EG Lab [14:20]

Минимальная дизъюнктивная нормальная форма (МДНФ) для логической функции — дизъюнкция с минимальным числом элементарных конъюнкций с минимальным числом аргументов (либо самих, либо их отрицаний) данной функции.

Для логической функции таблицы истинности и МДНФ совпадают.

Минимальная дизъюнктивная нормальная форма для логической функции с числом аргументов до четырёх может быть построена с помощью карт Карно. Для этого единицы карты Карно последовательно покрываются прямоугольниками 4×2, 2×4, 2×2, 4×1, 1×4, 2×1, 1×2 и 1×1. Затем строятся элементарные конъюнкты МДНФ.

Обозначения

n — число аргументов функции;

k — число прямоугольников на карте Карно;

(x₁,x₂,…,x_n) — набор аргументов функции;

f(x₁,x₂,…,x_n) — логическая функция;

P_t(x₁,x₂,…,x_n)={(i₁,l₁); (i₂,l₂); …; (i_m,l_m)} — множество клеток t-прямоугольника;

P_t(x₁,x₂,…,x_n)=1 — множество клеток t-прямоугольника из единиц;

arg_j(i, l) — значение аргумента x_j в наборе аргументов для клетки (i, l);

f_МДНФ(x₁,x₂,…,x_n) — МДНФ логической функции.

Формула

$f_{\text{МДНФ}}(x_{1},x_{2},\ldots ,x_{n})=\bigcap \limits _{t=1}^{k}\bigcap \limits _{\begin{smallmatrix}\arg _{j}\left[P_{t}(x_{1},x_{2},\ldots ,x_{n})=1\right]=1&{\text{или}}\\\arg _{j}\left[P_{t}(x_{1},x_{2},\ldots ,x_{n})=1\right]=0&\end{smallmatrix}}y_{j},$ где

$y_{j}={\begin{cases}x_{j},{\text{если}}\ \arg _{j}\left[P_{t}(x_{1},x_{2},\ldots ,x_{n})=1\right]=1\\{\bar {x}}_{j},{\text{если}}\ \arg _{j}\left[P_{t}(x_{1},x_{2},\ldots ,x_{n})=1\right]=0\end{cases}}$

$\arg _{j}\left[P_{t}(x_{1},x_{2},\ldots ,x_{n})=1\right]={\begin{cases}1,{\text{если}}\ \forall (i,l)\in P_{t}(x_{1},x_{2},\ldots ,x_{n}),\arg _{j}(i,l)=1\\0,{\text{если}}\ \forall (i,l)\in P_{t}(x_{1},x_{2},\ldots ,x_{n}),\arg _{j}(i,l)=0\end{cases}}$

Примеры построения МДНФ

Пример 1

Строим карту Карно для функции трёх переменных:

f(x₁,x₂,x₃)=(01001101)

Единицы карты Карно минимально покрываются одним прямоугольником вида 1×2 и двумя прямоугольниками вида 2×1, что соответствует трём элементарным конъюнкциям двух аргументов. Заметим, что два неполных прямоугольника вида 2×1 соответствуют одному полному прямоугольнику покрытия.

P₁(x₁,x₂,x₃)={(1,2);(4,2)}

P₂(x₁,x₂,x₃)={(3,2);(4,2)}

P₃(x₁,x₂,x₃)={(4,1);(4,2)}

$f_{\text{МДНФ}}(x_{1},x_{2},x_{3})=(x_{1}\land {\bar {x}}_{2})\lor (x_{1}\land x_{3})\lor ({\bar {x}}_{2}\land x_{3})$

Пример 2

Строим карту Карно для функции четырёх переменных:

f(x₁,x₂,x₃,x₄) = (1111110110100000)

Единицы карты Карно минимально покрываются тремя квадратами вида 2×2, что соответствует трём элементарным конъюнкциям двух аргументов. Заметим, что четыре угловых неполных квадрата соответствуют одному полному квадрату покрытия.

P₁(x₁,x₂,x₃,x₄)={(1,1);(1,4);(4,1);(4,4)}

P₂(x₁,x₂,x₃,x₄)={(1,1);(1,2);(2,1);(2,2)}

P₃(x₁,x₂,x₃,x₄)={(1,2);(1,3);(2,2);(2,3)}

$f_{\text{МДНФ}}(x_{1},x_{2},x_{3},x_{4})=({\bar {x}}_{1}\land {\bar {x}}_{3})\lor ({\bar {x}}_{1}\land x_{4})\lor ({\bar {x}}_{2}\land {\bar {x}}_{4})$

Пример 3

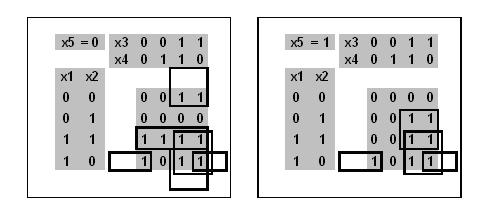
Строим трёхмерную карту Карно для функции пяти переменных:

f(x₁,x₂,x₃,x₄,x₅) = (00001010000001011100111110101111)

Единицы трёхмерной карты Карно минимально покрываются параллелепипедами вида 2×2×2, 2×2×1 (два), 1×4×1, 1×2×2, что соответствует одной элементарной конъюнкции двух аргументов и четырём элементарным конъюнкциям трёх аргументов. Заметим, что крайние по сторонам и угловые фигуры объединяются.

P₁(x₁,x₂,x₃,x₄,x₅)={(3,3,1);(3,4,1);(4,3,1);(4,4,1);(3,3,2);(3,4,2);(4,3,2);(4,4,2)}

P₂(x₁,x₂,x₃,x₄,x₅)={(1,3,1);(1,4,1);(4,3,1);(4,4,1)}

P₃(x₁,x₂,x₃,x₄,x₅)={(2,3,2);(2,4,2);(3,3,2);(3,4,2)}

P₄(x₁,x₂,x₃,x₄,x₅)={(3,1,1);(3,2,1);(3,3,1);(3,4,1)}

P₅(x₁,x₂,x₃,x₄,x₅)={(4,1,1);(4,4,1);(4,1,2);(4,4,2)}

$f_{\text{МДНФ}}(x_{1},x_{2},x_{3},x_{4},x_{5})=(x_{1}\land x_{3})\lor (x_{2}\land x_{3}\land x_{5})\lor ({\bar {x}}_{2}\land x_{3}\land {\bar {x}}_{5})\lor (x_{1}\land x_{2}\land {\bar {x}}_{5})\lor (x_{1}\land {\bar {x}}_{2}\land {\bar {x}}_{4})$

Другие формы:

1. совершенная дизъюнктивная нормальная форма;
2. совершенная конъюнктивная нормальная форма;
3. минимальная дизъюнктивная нормальная форма;
4. минимальная конъюнктивная нормальная форма);
5. алгебраическая нормальная форма.