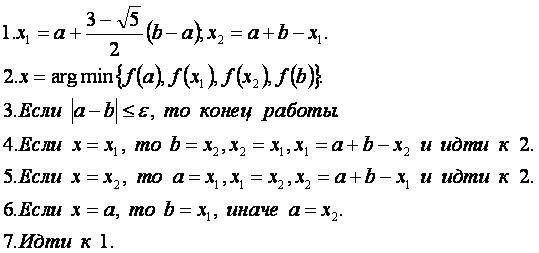Метод золотого сечения
Метод золотого сечения — это численный метод нахождения решения x (с заданной точностью ε), минимизирующего функцию f(x) на отрезке.
Описание метода[править]
Суть метода золотого сечения состоит в разбиении отрезка [a,b] на три отрезка в пропорции золотого сечения, определении минимального значения функции f(x) из значений на границах этих отрезков и выборе нового отрезка, на котором функция содержит минимизирующее решение.
Деление отрезка продолжается до достижения необходимой точности решения ε.
Сначала находим отрезок [a,b] такой, что функция f(x) непрерывна и вогнута на отрезке, то есть f"(x)>0.
Далее применяем алгоритм.
Алгоритм[править]
Входные данные: f(x), a, b, ε.
Выходные данные: x.
Значение x является минимизирующим решением для функции f(x) с заданной точностью ε.
- Заметим, что для нахождения решения x, максимизирующего выпуклую функцию f(x) на отрезке, алгоритм решения модифицируется в части строки 2, она меняется на строку вида:
Другие методы:[править]
Ссылки[править]
- Википедия
- Участник:Logic-samara
 Методы оптимизации ↑ [+] | |
|---|---|
| Одномерные |
Метод золотого сечения • Дихотомия • Метод парабол • Перебор по сетке • Метод равномерного блочного поиска • Метод Фибоначчи • Троичный поиск • Метод Пиявского |
| Прямые методы |
Метод Гаусса • Метод Нелдера — Мида • Метод сопряжённых направлений • Метод Хука — Дживса • Метод конфигураций • Метод Розенброка |
| Первого порядка |
Градиентный спуск • Метод Зойтендейка • Покоординатный спуск • Метод сопряжённых градиентов • Квазиньютоновские методы • Алгоритм Левенберга — Марквардта |
| Второго порядка |
Метод Ньютона • Метод Ньютона — Рафсона • Алгоритм Бройдена — Флетчера — Гольдфарба — Шанно (BFGS) |
| Стохастические |
Метод Монте-Карло • Имитация отжига • Эволюционные алгоритмы • Дифференциальная эволюция • Муравьиный алгоритм • Метод роя частиц |
| Методы линейного программирования |
Симплекс-метод • Алгоритм Гомори • Метод эллипсоидов • Метод потенциалов |
| Методы нелинейного программирования | |