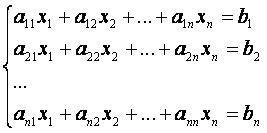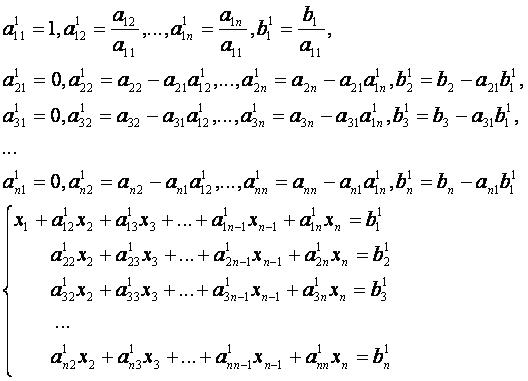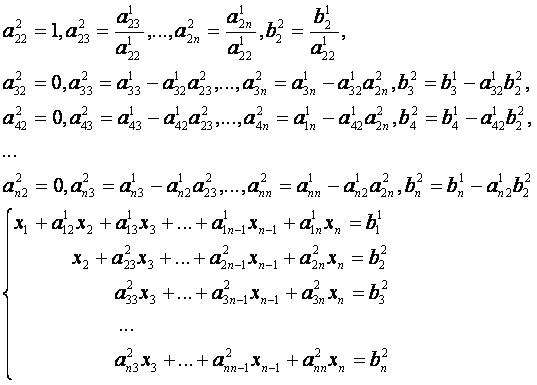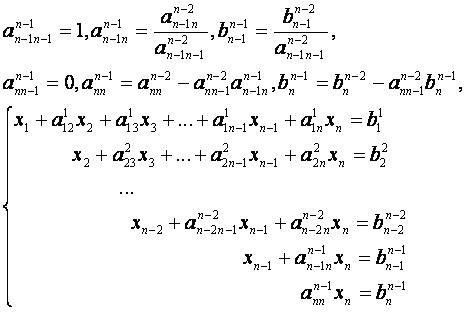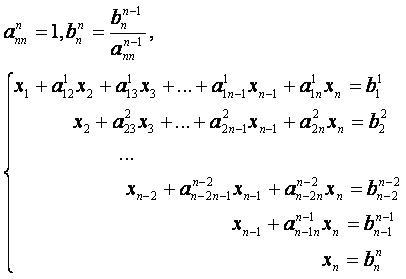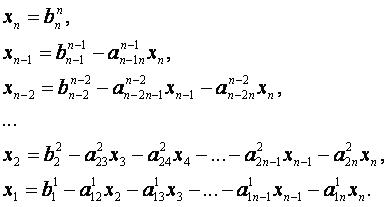Метод Гаусса
Метод Гаусса — это численный метод нахождения решения системы линейных уравнений вида Ax=b.
Описание метода[править]
Суть метода Гаусса состоит в приведении системы уравнений к треугольному виду с помощью элементарных преобразований строк.
Алгоритм решения[править]
Входные данные: A, b.
Прямой ход.
...
Обратный ход.
Выходные данные: x.
См. также[править]
Другие методы:[править]
- Для решения систем нелинейных уравнений используется метод Ньютона.
Ссылки[править]
- Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Наука, 1970.
- Участник:Logic-samara
 Методы оптимизации ↑ [+] | |
|---|---|
| Одномерные |
Метод золотого сечения • Дихотомия • Метод парабол • Перебор по сетке • Метод равномерного блочного поиска • Метод Фибоначчи • Троичный поиск • Метод Пиявского |
| Прямые методы |
Метод Гаусса • Метод Нелдера — Мида • Метод сопряжённых направлений • Метод Хука — Дживса • Метод конфигураций • Метод Розенброка |
| Первого порядка |
Градиентный спуск • Метод Зойтендейка • Покоординатный спуск • Метод сопряжённых градиентов • Квазиньютоновские методы • Алгоритм Левенберга — Марквардта |
| Второго порядка |
Метод Ньютона • Метод Ньютона — Рафсона • Алгоритм Бройдена — Флетчера — Гольдфарба — Шанно (BFGS) |
| Стохастические |
Метод Монте-Карло • Имитация отжига • Эволюционные алгоритмы • Дифференциальная эволюция • Муравьиный алгоритм • Метод роя частиц |
| Методы линейного программирования |
Симплекс-метод • Алгоритм Гомори • Метод эллипсоидов • Метод потенциалов |
| Методы нелинейного программирования | |