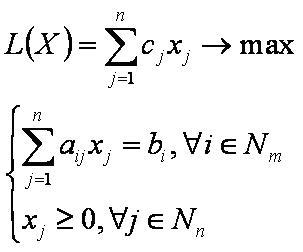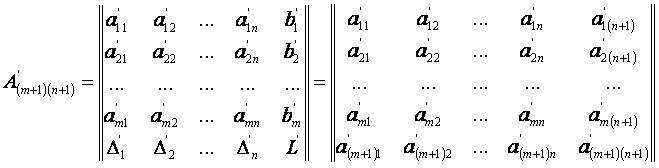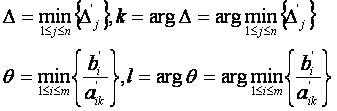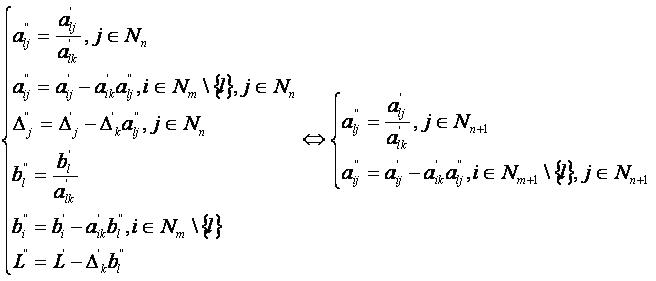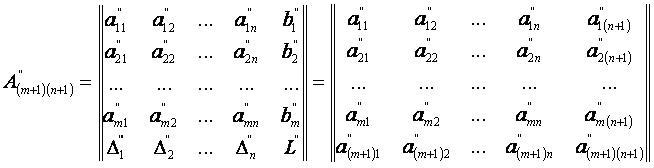Симплекс-метод
Симплекс-метод — метод для решения задач линейного программирования канонического вида, т.е. задач с ограничениями в форме равенств.
Описание метода[править]
Суть симплекс-метода состоит в переходе от одной угловой точки (одного базиса) многогранника допустимых решений к другой (другому базису) с целью оптимизации целевой функции. При этом симплекс-таблица в каждом базисе новая. Целевая функция соответствует гиперплоскости (в заданном базисе), которая проходит через угловую точку. Оценки оптимальности соответствуют отклонениям относительно гиперплоскости. Когда все оценки оптимальности положительны, тогда целевая функция достигает максимума, когда все оценки оптимальности отрицательны, тогда целевая функция достигает минимума.
Каноническая задача[править]
Математическая модель канонической задачи имеет следующий вид:
или
В каждой угловой точке многогранника допустимых решений число базисных элементов совпадает с числом (независимых) уравнений. Симплекс-таблица для базисных элементов имеет единичные вектор-столбцы.
Расширенная матрица[править]
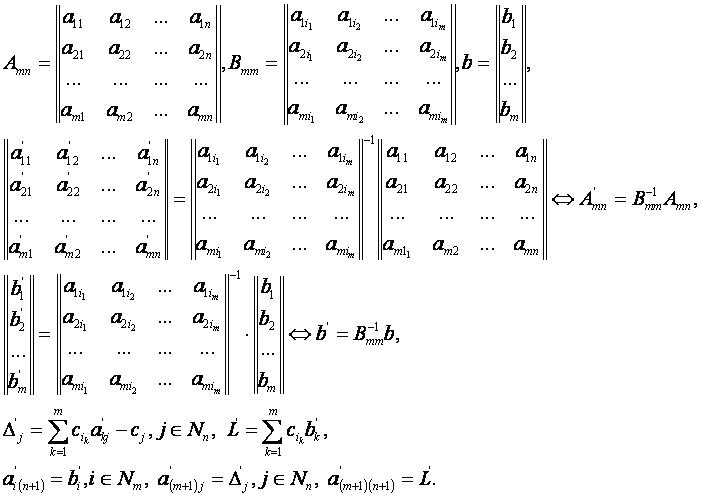
Для построения симплекс-таблицы, необходимо выбрать базисные элементы, построить из базисных вектор-столбцов матрицы коэффициентов A базисную матрицу B. Затем рассчитать матрицу коэффициентов A’ по формулам и построить расширенную матрицу.
Расширенная матрица исходной симплекс-таблицы имеет вид:
Симплекс-таблица[править]
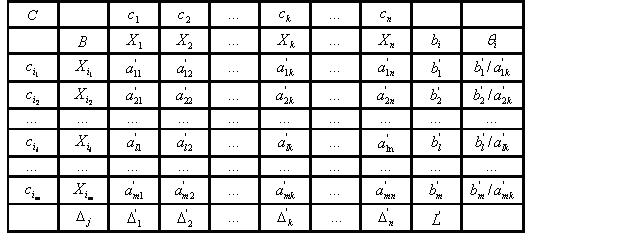
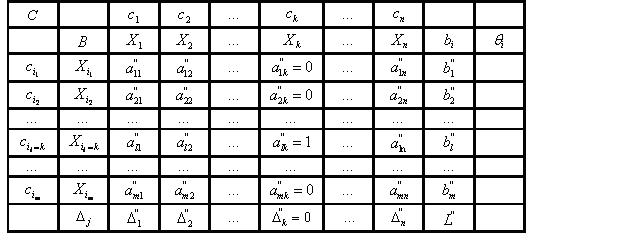
Исходная симплекс-таблица имеет вид:
Формулы выбора переменных для ввода в базис и для вывода из базиса
В случае когда Δ=0, опорное решение X - оптимальное и завершение итераций, иначе строится новая симплекс-таблица с новым опорным решением.
Формулы перехода к новой симплекс-таблице имеют вид:
Расширенная матрица новой симплекс-таблицы имеет вид:
Новая симплекс-таблица имеет вид:
Далее переходят к выбору новых переменных для ввода в базис и для вывода из базиса.
- Заметим, что при решении задачи максимизации при выборе новой переменной выбирают минимальную оценку Δj, чтобы избавиться от всех отрицательных оценок Δj. При решении задачи минимизации при выборе новой переменной надо выбирать максимальную оценку Δj, чтобы избавиться от всех положительных оценок Δj. Оценки Δj называются критериями оптимальности.
Другие методы:[править]
Литература[править]
- Юдин Д. Б., Гольштейн Е. Г. Линейное программирование — М.,1963.
Ссылки[править]
Методы оптимизации ↑ | |
|---|---|
| Одномерные |
Метод золотого сечения • Дихотомия • Метод парабол • Перебор по сетке • Метод равномерного блочного поиска • Метод Фибоначчи • Троичный поиск • Метод Пиявского |
| Прямые методы |
Метод Гаусса • Метод Нелдера — Мида • Метод сопряжённых направлений • Метод Хука — Дживса • Метод конфигураций • Метод Розенброка |
| Первого порядка |
Градиентный спуск • Метод Зойтендейка • Покоординатный спуск • Метод сопряжённых градиентов • Квазиньютоновские методы • Алгоритм Левенберга — Марквардта |
| Второго порядка |
Метод Ньютона • Метод Ньютона — Рафсона • Алгоритм Бройдена — Флетчера — Гольдфарба — Шанно (BFGS) |
| Стохастические |
Метод Монте-Карло • Имитация отжига • Эволюционные алгоритмы • Дифференциальная эволюция • Муравьиный алгоритм • Метод роя частиц |
| Методы линейного программирования |
Симплекс-метод • Алгоритм Гомори • Метод эллипсоидов • Метод потенциалов |
| Методы нелинейного программирования | |