Семеричная система счисления
Семеричная система (7-ричная система) — позиционная система счисления с основанием 7.
Обозначения:[править]
a7 – натуральное число в семеричной системе счисления;
a10 – натуральное число в десятичной системе счисления;
n – число цифр в числе a7;
bj_7 – j-тая (справа-налево) семеричная цифра числа a7, принимает значения цифр от 0 до 6;
bj_10 – десятичное число соответствующее j-той (справа-налево) семеричной цифре числа a7, принимает значения от 0 до 6.
Формула числа[править]
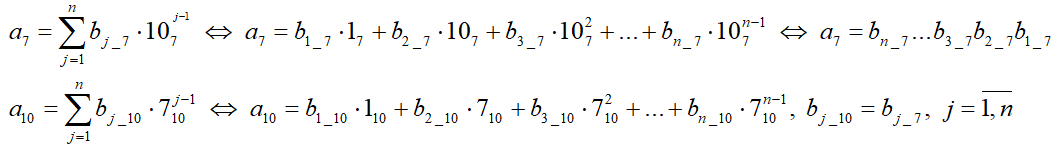 С помощью n позиций в семеричной системе счисления можно записать целые числа в диапазоне от 0 до 7n-1, то есть всего 7n различных чисел.
С помощью n позиций в семеричной системе счисления можно записать целые числа в диапазоне от 0 до 7n-1, то есть всего 7n различных чисел.
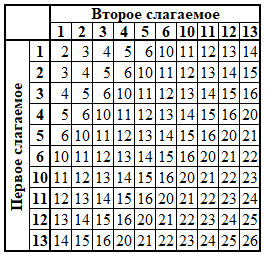
Таблицы сложения:[править]
Таблица сложения в семеричной системе счисления[править]
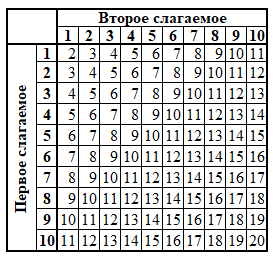
Таблица сложения в десятичной системе счисления[править]
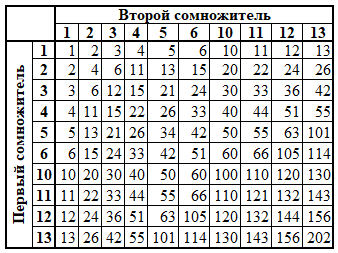
Таблицы умножения:[править]
Таблица умножения в семеричной системе счисления[править]
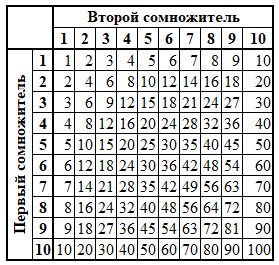
Таблица умножения в десятичной системе счисления[править]
Другие системы счисления:[править]
- двоичная (цифры:0-1);
- троичная (цифры:0-2);
- четверичная (цифры:0-3);
- пятеричная (цифры:0-4);
- шестеричная (цифры:0-5);
- семеричная (цифры:0-6);
- восьмеричная (цифры:0-7);
- девятеричная (цифры:0-8);
- десятичная (цифры:0-9);
- одиннадцатиричная (цифры:0-9,A);
- одиннадцатиричная специальная (цифры:0-9,A);
- двенадцатеричная (цифры:0-9,A-B);
- тринадцатеричная (цифры:0-9,A-C);
- четырнадцатеричная (цифры:0-9,A-D);
- пятнадцатеричная (цифры:0-9,A-E);
- шестнадцатеричная (цифры:0-9,A-F).
Примеры алгоритмов:[править]
Перевод из семеричной системы счисления в десятичную[править]
Считается сумма произведений цифр семеричной системы счисления на веса разрядов (основание 7 в степени номер разряда, начиная с нулевого; нулевой разряд это разряд единиц, далее разряды десятков, сотен, тысяч и т.д.) в семеричной системе. Полученное число является записью исходного числа в десятичной системе счисления.
Перевод 7→10[править]
41247=4˙73+1˙72+2˙71+4˙70=4˙343+1˙49+2˙7+4˙1=1372+49+14+4=143910 => 41247=143910
Перевод из десятичной системы счисления в семеричную[править]
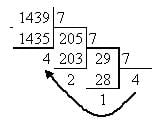
Сначала производится последовательное деление столбиком исходного числа и получаемых (от предыдущих делений) частных (больших или равных основанию) на основание 7 и записываются остатки от делений. Деление продолжается до тех пор, пока частное не станет меньше основания 7. Затем выписываются цифры в семеричной системе счисления вместо последнего частного и остатков от делений в обратном (получению) порядке. Полученное число является записью исходного числа в семеричной системе счисления.
Перевод 10→7[править]
Другие системы счисления:[править]
- двоичная (цифры:0-1);
- троичная (цифры:0-2);
- четверичная (цифры:0-3);
- пятеричная (цифры:0-4);
- шестеричная (цифры:0-5);
- семеричная (цифры:0-6);
- восьмеричная (цифры:0-7);
- девятеричная (цифры:0-8);
- десятичная (цифры:0-9);
- одиннадцатиричная (цифры:0-9,A);
- одиннадцатиричная специальная (цифры:0-9,A);
- двенадцатеричная (цифры:0-9,A-B);
- тринадцатеричная (цифры:0-9,A-C);
- четырнадцатеричная (цифры:0-9,A-D);
- пятнадцатеричная (цифры:0-9,A-E);
- шестнадцатеричная (цифры:0-9,A-F).