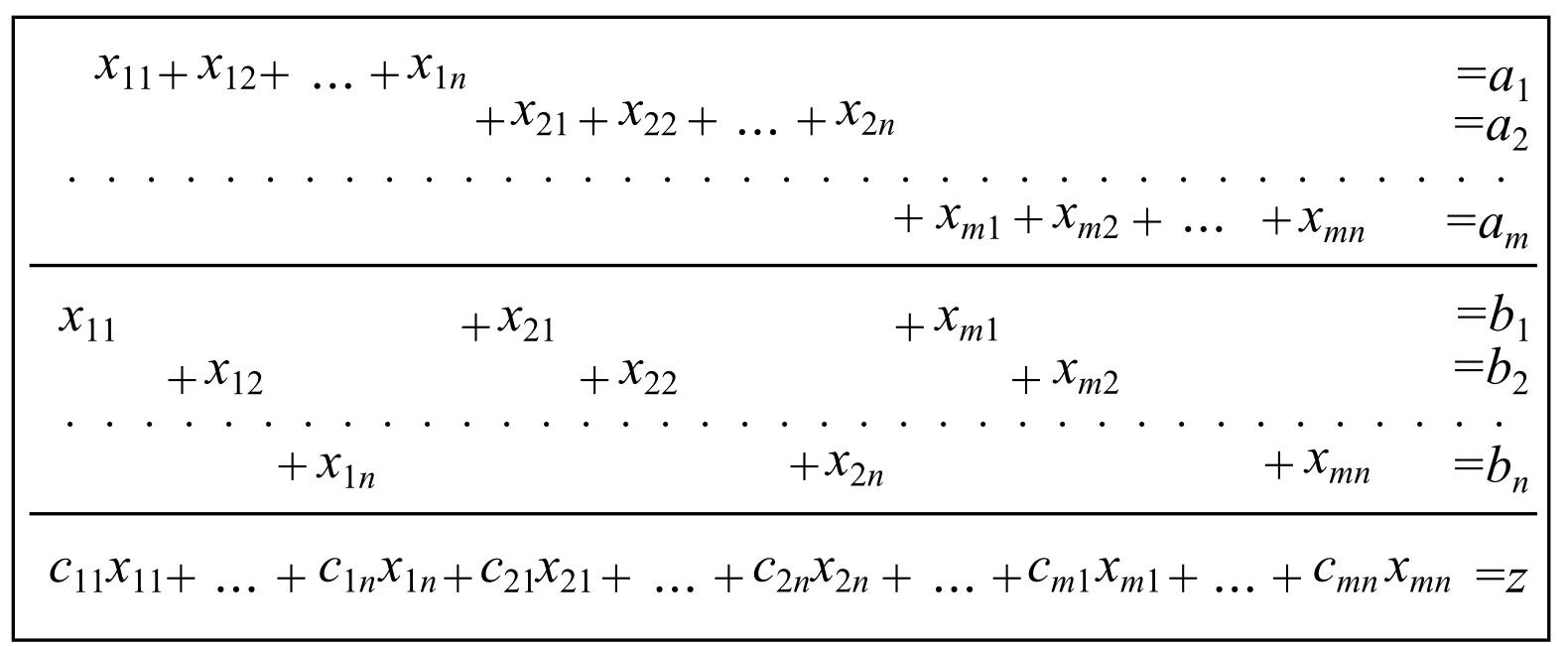Транспортная задача
Транспортная задача в формальной науке — это класс задач по «нахождению» — вычислению — оптимального распределения поставок однородного абстрактного «груза» между пунктами отправления и назначения при заданных численно выраженных стоимостях перевозки. Первое в истории общее решение было представлено методами линейной алгебры, — как для задачи линейного программирования специального вида. Транспортная задача может быть представлена на письме в виде прямоугольной таблицы. Пример такой записи для конкретной транспортной задачи:
| Потребитель B1, потребность 20 кг |
Потребитель B2, потребность 30 кг |
Потребитель B3, потребность 30 кг |
Потребитель B4, потребность 10 кг | |
|---|---|---|---|---|
| Поставщик A1, запас 30 кг |
С11=2 руб./кг | С12=3 руб./кг | С13=2 руб./кг | С14=4 руб./кг |
| Поставщик A2, запас 40 кг |
С21=3 руб./кг | С22=2 руб./кг | С23=5 руб./кг | С24=1 руб./кг |
| Поставщик A3, запас 20 кг |
С31=4 руб./кг | С32=3 руб./кг | С33=2 руб./кг | С34=6 руб./кг |
Цена перевозки (например, в рублях за 1 килограмм груза) Cij записывается в ячейки таблицы на пересечении соответствующего потребителя и поставщика (цена может быть и отрицательной — в этом случае она представляет собой прибыль).[1]
Неизвестной (искомой) величиной в задаче являются такие объемы перевозки xij от поставщиков к потребителям, чтобы минимизировать общие затраты на транспортировку.[2][3]. В табличной записи цены отделяют от объемов перевозки косой чертой или квадратным уголком, в этой статье из соображений лучшей доходчивости они подписаны. При решении транспортной задачи единственными необходимыми арифметическими действиями являются сложение и вычитание.[1] Для поиска начального решения применяют метод северо-западного угла,![]() метод минимальных тарифов
метод минимальных тарифов ![]() или метод Фогеля,
или метод Фогеля, ![]() а для окончательной оптимизации — метод потенциалов.
а для окончательной оптимизации — метод потенциалов. ![]() В то же время, транспортная задача является подмножеством задач линейного программирования и может решаться симплекс-методом.
В то же время, транспортная задача является подмножеством задач линейного программирования и может решаться симплекс-методом.![]() [1] Транспортную задачу можно решать также в программах автоматизации электронных таблиц, как Excel.
[1] Транспортную задачу можно решать также в программах автоматизации электронных таблиц, как Excel. ![]()
Историческая справка[править]
Проблема была формализована французским математиком Гаспаром Монжем в 1781 г.[5] Согласно публикации Александера Шривьера[6] первым, кто изучал транспортную задачу математически, был некто «А. Н. Толстой» из СССР. В 1930 г. вышла его работа о поиске минимального общего километража в железнодорожных перевозках,[7], дополненная им же в публикации 1939 года[8]. где использовались перераспределительные циклы.[4] В биографиях писателя Алексея Николаевича Толстого не упоминается какое-либо его занятие, связанное с передовыми исследованиями по логистике или математике, — вероятно, это тёзка.
По сведениям Гасса[2], задача такого вида в западной литературе впервые была поставлена Хичкоком в 1941 г.[9] и детально разобрана Купмансом[10], который работал членом Объединенного комитета перевозок во время Второй мировой войны, когда недостаток грузовых судов представлял собой критическое узкое место.[11] Как проблему линейного программирования (детализация симплекс-метода) ее впервые рассмотрел Джордж Данциг.[11] Другой процесс вычисления («метод одновременного решения прямой и двойственной задач») был предложен Фордом и Фулкерсоном в 1956 г.[12][11] Способ решения транспортной задачи (методом потенциалов) в СССР был опубликован Канторовичем и Гавуриным в 1949 г.[13] и ранее. В своей книге «Линейное программирование, его применения и обобщения» (М.: Соцэкгиз, 1966) Данциг ссылается на публикации Канторовича 1939 г.[14] и 1942 г.[15], а также последующую статью 1949 г.,[13] содержащие, как он считал, в завершенном виде теорию задачи о перевозках, хотя и с неполным вычислительным алгоритмом, написанные на доступном для расчетчиков языке. К сожалению, по его мнению, эти работы оказались малоизвестными в СССР и за его пределами.[1] В противоположность этому, сам Канторович в своих мемуарах 1987 г. утверждал, что университет немедленно опубликовал его статью, и она была разослана в пятьдесят Народных комиссариатов.[4] По сведениям Данцига, для ЭВМ программа симплекс-метода для случая решения транспортной задачи[16] была впервые разработана в 1950 г. для машины СЕАК, а программа для общего симплекс-метода — в 1951 г. под руководством А. Ордена из ВВС США и А. Д. Гофмана из Бюро стандартов.[1]
Балансировка задачи[править]
Если сумма запасов равна сумме потребностей,[17] то транспортная задача называется закрытой. Если равенство не соблюдается, то задача называется открытой. Для решения транспортной задачи необходимо, чтобы она была приведена к закрытому виду.[18]
В показанном выше примере, сумма запасов = 30 + 40 + 20 = 90 кг, а сумма потребностей = 20 + 30 + 30 + 10 кг = 90 кг (запасы и потребности равны между собой, задача закрытая).
Если это равенство не соблюдено, необходимо ввести фиктивного поставщика или фиктивного потребителя на недостающий или избыточный объем товара, которому нужно приписать нулевую цену доставки. Этот объем будет соответствовать недопоставке или, напротив, избытку товара на складе.[3]
Поиск начального решения[править]
Решение транспортной задачи начинается с поиска допустимого начального решения (плана перевозок), чтобы все запасы поставщиков были распределены по потребителям. Допустимое начальное решение не обязательно оказывается оптимальным, а метод его нахождения может быть как простейшим (метод северо-западного угла или аналоги) или более сложным и приближенным к оптимальному решению (метод минимальных тарифов, метод Фогеля)[19], или же вообще произвольным. [20]
Метод северо-западного угла[править]
Допустимое (но не всегда оптимальное с точки зрения стоимости доставки) начальное решение транспортной задачи можно построить, последовательно перебирая строки таблицы (то есть поставщиков) сверху вниз. В пределах каждой строки нужно перебрать слева направо не охваченных или не полностью охваченных поставками потребителей, записывая в соответствующие ячейки объем поставляемого груза от поставщика в данной строке, и так до исчерпания возможностей поставщика. Таким образом, весь груз от поставщиков будет распределен по потребителям. Этот метод был предложен Данцигом в 1951 г.[11] и назван Чарнесом и Купером[21] «правилом северо-западного угла».[2]
| B1, 20 кг | B2, 30 кг | B3, 30 кг | B4, 10 кг | |
|---|---|---|---|---|
| A1, 30 кг | X11=20 кг | Х12=10 кг | ||
| A2, 40 кг | Х22=20 кг | Х23=20 кг | ||
| A3, 20 кг | Х33=10 кг | Х34=10 кг |
В таблице здесь и далее зеленым цветом отмечены ячейки с ненулевыми объемами перевозки груза (базисные ячейки).[22] Подробности см. в статье Метод северо-западного угла.
Метод минимальных тарифов[править]
Другой метод получения начального решения — записывать отгрузки в первую очередь в те ячейки, где тариф минимален. Этот метод позволяет получить более приближенное к оптимальному решение, которое, однако, может потребовать дальнейшей оптимизации.[3] Метод минимальных тарифов с его модификациями (минимальный тариф по строке или минимальный тариф по столбцу) был описан Данцигом в работе 1951 г.[11] Подробнее см. в статье Метод минимальных тарифов.
Метод Фогеля[править]
Для поиска начального решения транспортной задачи можно применить также метод Фогеля, который обычно дает еще более приближенное к оптимальному решение. Подробнее см. в статье Метод Фогеля.
Решение транспортной задачи методом потенциалов[править]
Метод потенциалов позволяет за несколько шагов (итераций) найти полностью оптимальное решение транспортной задачи. Перед решением задачи этим методом нужно найти допустимое начальное решение одним из методов, описанных в разделе выше. ![]() Поскольку у нас нет ограничений на черно-белую полиграфию, для большей ясности ячейки транспортной таблицы в этой статье отмечены разными цветами.
Поскольку у нас нет ограничений на черно-белую полиграфию, для большей ясности ячейки транспортной таблицы в этой статье отмечены разными цветами.
1. Проверка правильности распределения объемов[править]
Эта проверка не входит в алгоритм метода потенциалов, но может потребоваться для исключения арифметических ошибок (при ручном расчете на бумаге) или самопроверки алгоритма при компьютерных вычислениях. Особенностью распределения груза по транспортной таблице является совпадение суммы объемов по строкам с запасами соответствующего поставщика, а суммы объемов по столбцам — с потребностями соответствующих потребителей. [23][1]
В показанном выше примере,
- Для 1-й строки: 30 кг = 20 + 10 кг
- Для 2-й строки: 40 кг = 20 + 20 кг
- Для 3-й строки: 20 кг = 10 + 10 кг
- Для 1-го столбца: 20 кг = 20 кг
- Для 2-го столбца: 30 кг = 10 + 20 кг
- Для 3-го столбца: 30 кг = 20 + 10 кг
- Для 4-го столбца: 10 кг = 10 кг
2. Вычисление общей стоимости транспортировки[править]
Этот шаг также не входит в сам алгоритм метода потенциалов, но он полезен для распечатки результатов и показа, что алгоритм движется в правильном направлении, уменьшая на каждом (или не на каждом) шаге общую себестоимость перевозки. Для всех ячеек цена умножается на объем перевозки и полученный результат суммируется.[24][3]
| B1, 20 кг | B2, 30 кг | B3, 30 кг | B4, 10 кг | |
|---|---|---|---|---|
| A1, 30 кг | С11=2 руб./кг, X11=20 кг |
С12=3 руб./кг, Х12=10 кг |
С13=2 руб./кг | С14=4 руб./кг |
| A2, 40 кг | С21=3 руб./кг | С22=2 руб./кг, Х22=20 кг |
С23=5 руб./кг, Х23=20 кг |
С24=1 руб./кг |
| A3, 20 кг | С31=4 руб./кг | С32=3 руб./кг | С33=2 руб./кг, Х33=10 кг |
С34=6 руб./кг, Х34=10 кг |
В нашем примере, сумма затрат на перевозку груза составляет
2×20 + 3×10 + 2×20 + 5×20 + 2×10 + 6×10 = 290 руб.
3. Разделение ячеек на базисные и свободные[править]
Ячейки (клетки) транспортной таблицы с ненулевыми перевозками называются базисными, а клетки с нулевыми объемами перевозки — свободными.[18]
4. Проверка плана на вырожденность[править]
→ Вырожденность в транспортной задаче
Базисных (см. выше) ячеек таблицы должно быть не менее m+n-1, где m и n — соответственно, число поставщиков и потребителей, иначе решение считается вырожденным и требует введения в базис одной из ячеек с нулевой перевозкой[19] (чтобы алгоритм не впал в бесконечный цикл, эта ячейка должна быть случайной).[1] Для исключения ситуаций с вырожденностью к объемам потребления добавляют небольшие возмущения — числа, заведомо ничтожные при перевозках (такие как 0.00001), при этом к объему поставки одного из поставщиков добавляют их сумму (или наоборот).[1][2]
5. Вычисление потенциалов[править]
Каждому поставщику Ai соответствует потенциал Ui, а каждому потребителю Bj соответствует потенциал Vj. Данциг называет потенциалы Ui и Vj симплекс-множителями или неявными ценами.[1] Чтобы определить эти потенциалы, полагают, что U1=0, а остальные потенциалы вычисляют из соотношения
Ui + Vj = Cij
для всех занятых (базисных) ячеек таблицы (отмечены зеленым).[3]
| V1 | V2 | V3 | V4 | |
|---|---|---|---|---|
| U1=0 | С11=2 руб./кг | С12=3 руб./кг | ||
| U2 | С22=2 руб./кг | С23=5 руб./кг | ||
| U3 | С33=2 руб./кг | С34=6 руб./кг |
U1+V1=2. Поскольку U1=0, 0+V1=2, следовательно, V1=2 руб./кг
U1+V2=3. Поскольку U1=0, 0+V2=3, следовательно, V2=3 руб./кг
U2+V2=2. Поскольку V2=3, U2+3=2, следовательно, U2=–1 руб./кг
U2+V3=5. Поскольку U2=–1, –1+V3=5, следовательно, V3=6 руб./кг
U3+V3=2. Поскольку V3=6, U3+6=2, следовательно, U3=–4 руб./кг
U3+V4=6. Поскольку U3=–4, –4+V4=6, следовательно, V4=10 руб./кг
При компьютерной реализации удобно использовать рекурсию: взаимный вызов двух функций, которые отрабатывают алгоритм, соответственно, по строкам и по столбцам. Если на предыдущем шаге 4 (в разделе «Проверка плана на вырожденность») ![]() в базис была введена случайная не занятая ячейка (без проверки ее на ацикличность), то вычисление u и v может дать сбой, и в этом случае случайный выбор вводимой в базис нулевой ячейки на предыдущем шаге 4 следует повторить.
в базис была введена случайная не занятая ячейка (без проверки ее на ацикличность), то вычисление u и v может дать сбой, и в этом случае случайный выбор вводимой в базис нулевой ячейки на предыдущем шаге 4 следует повторить.
6. Проверка решения на оптимальность[править]
Для всех незанятых ячеек (с нулевым объемом перевозки) вычисляют оценки клеток распределительной таблицы Δij по формуле Δij = Сij – Ui – Vj, где Ui и Vj берутся из вычислений, выполненных в разделе выше (здесь они вписаны в заголовки таблицы).[3]
Для всех занятых ячеек (с ненулевыми объемами перевозки, отмечены зеленым цветом) полагают Δij=0, поскольку на следующем шаге нам потребуется значение с минимальной оценкой в незанятых ячейках.[3]
| V1=2 | V2=3 | V3=6 | V4=10 | |
|---|---|---|---|---|
| U1=0 | Δ11=0 | Δ12=0 | Δ13 = 2–0–6 = –4 | Δ14=4–0–10 = –6 |
| U2=–1 | Δ21=3–(–1)–2 = 2 | Δ22=0 | Δ23=0 | Δ24=1–(–1)–10 = –8 |
| U3=–4 | Δ31=4–(–4)–2 = 6 | Δ32=3–(–4)–3 = 4 | Δ33=0 | Δ34=0 |
Если в получившейся таблице нет отрицательных значений Δij, то план перевозок оптимален и задача решена (переход к шагу 10).![]()
В нашем примере есть отрицательные значения. Наличие отрицательных значений Δij означает, что решение не оптимально.[3]
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
| A1 | Δ11=0 | Δ12=0 | Δ13=–4 | Δ14=–6 |
| A2 | Δ21=2 | Δ22=0 | Δ23=0 | Δ24=–8 |
| A3 | Δ31=6 | Δ32=4 | Δ33=0 | Δ34=0 |
Наименьшее отрицательное значение Δ24=–8 (начальная вершина для цикла перераспределения поставок, о котором см. ниже)[3] отмечено красным цветом. Если одинаковых отрицательных значений несколько, то берется любое[20] [25]
7. Построение цикла[править]

Цикл перераспределения поставок представляет собой замкнутую ломаную линию, которая соединяет начальную вершину (отмечена красным цветом) и занятые (отмеченные в нашем примере зеленым цветом) ячейки транспортной таблицы по определенным правилам.[3]
- Все вершины, кроме начальной, находятся в занятых ячейках таблицы (ячейки с ненулевыми перевозками или «введенные в базис» на шаге 4 (в разделе «Проверка плана на вырожденность» ячейки с нулевой перевозкой — здесь они отмечены в примерах зеленым цветом), при этом охвачены циклом могут быть не все, а лишь некоторые занятые ячейки.[3]
- В каждой вершине цикла встречаются ровно два звена ломаной линии, причем одна из них находится по строке, а другая — по столбцу.[26] Иначе говоря, они пересекаются под прямым углом.[3]
- Линия может пересекать занятые ячейки, не включая их в цикл (включение их в цикл не допускается).[3] Другими словами, никакие три последовательные вершины не могут находиться в одной и той же строке или одном и том же столбце.[26]
- Линия может пересекать саму себя, при этом точка пересечения не включается в цикл (исходя из п.2).[26]
| B1, 20 кг | B2, 30 кг | B3, 30 кг | B4, 10 кг | |
|---|---|---|---|---|
| A1, 30 кг | X11=20 кг | Х12=10 кг | ||
| A2, 40 кг | Х22=20 кг | (*) Х23=20 кг | (*) | |
| A3, 20 кг | (*) Х33=10 кг | (*) Х34=10 кг |
Вершины цикла в этом примере помечены звездочкой (*). Горизонтальные и вертикальные линии, соединяющие вершины, в этом примере не показаны. По вершинам цикла нужно перераспределить объемы, чтобы получить следующее приближение к оптимальному решению задачи, как это показано далее.
При компьютерной реализации построения цикла удобно использовать рекурсию, то есть взаимный вызов двух функций, которые строят линии цикла по строкам и по столбцам, соответственно.[27]
8. Перераспределение поставок по циклу[править]
«Красной» ячейке цикла присваиваем знак (+), следующей по циклу (начать двигаться можно в любом направлении) — знак (–), следующей ячейке цикла — опять (+) и так далее. Находим минимальную поставку по отмеченным знаком (–) вершинам цикла и обозначаем ее θ. Эта вершина цикла Х34=10 кг помечена желтым цветом. Значение θ вычитаем из вершин цикла, которые помечены знаком (–) и прибавляем его к вершинам цикла, которые помечены знаком (+).[3][26]
| B1, 20 кг | B2, 30 кг | B3, 30 кг | B4, 10 кг | |
|---|---|---|---|---|
| A1, 30 кг | X11=20 кг | Х12=10 кг | ||
| A2, 40 кг | Х22=20 кг | (–) Х23=20 кг | (+) | |
| A3, 20 кг | (+) Х33=10 кг | (–) Х34=10 кг |
Получаем новое решение, которое чуть-чуть оптимальнее.
| B1, 20 кг | B2, 30 кг | B3, 30 кг | B4, 10 кг | |
|---|---|---|---|---|
| A1, 30 кг | X11=20 кг | Х12=10 кг | ||
| A2, 40 кг | Х22=20 кг | Х23=10 кг | Х24=10 кг | |
| A3, 20 кг | Х33=20 кг |
9. Зацикливание решения[править]
Поскольку алгоритм является циклическим (итерационным), переходим к пункту 1. ![]()
Примечание: есть опасность, что алгоритм впадет в бесконечный цикл из-за вырожденности или каких-либо ошибок реализации, поэтому полезно предусмотреть проверку на максимальное число шагов или максимальное время, которое будет исполняться программа (например, при поиске решения в Microsoft Excel эти параметры вынесены в пользовательские настройки). Впрочем, по мнению Данцига, те меры, которые можно предпринять для исключения вырожденности (см. Вырожденность в транспортной задаче) приводят к успеху в 100 % случаев. Для подстраховки можно применить метод Фогеля, который не склонен «впадать» в бесконечные циклы, и выдает более или менее приближенное к оптимальному решение за ограниченное число шагов.
10. PROFIT[править]
Сюда мы переходим из пункта 6, если решение было признано оптимальным.
Программная реализация[править]
Программа от Jean-Pierre Blanger, PSI Editions, France, 1982 содержит достаточно древний код на языке Basic,[28] версия на языке Pascal была реализована J-P Moreau, Paris.[29]. Реализация для 1С:Предприятие и Delphi 7 (адаптация кода от Blanger с обменом через XML) приведена по ссылке.[30] Код изобилует goto, но работоспособный, однако, в нем не учитывается возможность вырожденности и на некоторых задачах выдается ошибка «degenerate solution» (побороть можно простым прибавлением малых чисел — возмущений, см. выше). Реализация на языке Бейсик имеется в книге Б.Банди[31], однако, код в русском переводе не работоспособен. Реализация на языке Python (работающая) от James Coliins приведена по ссылке.[27] Для 1С:Предприятие 8.2 автором статьи был разработан оригинальный код с заимствованием некоторых идей и тестовых примеров от James Coliins, который приведен по ссылке.[32]
Решение симплекс-методом[править]
→ Решение транспортной задачи симплекс-методом
Транспортную задачу можно решать также симплекс-методом, выразив данные транспортной таблицы через линейные уравнения:[1]
Поиск решения в Excel[править]
→ Решение транспортной задачи в Excel
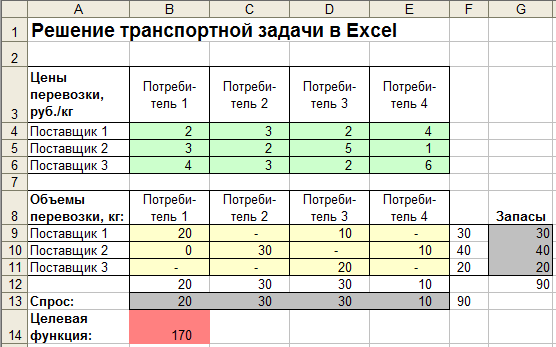
Для поиска оптимального решения транспортной задачи, а также проверки имеющихся программных средств на правильность можно использовать надстройку «Поиск решения» в Microsoft Excel.
Программа «склонна» выдавать вещественные объемы перевозок наподобие 4.99999 или 1E-26, которые перед показом пользователю подлежат округлению соответствующим форматированием ячеек Excel.
Excel выдает ошибку на таблицах определенной величины (из 2-3 десятков потребителей и поставщиков).
Математическая модель транспортной задачи[править]
Обобщения транспортной задачи[править]
Источники[править]
<references> [19] [3] [5] [4] [9] [10] [12] [13] [14] [15] [1] [16] [18] [11] [21] [2] [20] [26] [27] [31]
- ↑ 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 Дж. Данциг «Линейное программирование, его применения и обобщения» М:Прогресс, 1966 (djvu)
- ↑ 2,0 2,1 2,2 2,3 2,4 С.Гасс. Линейное программирование (методы и приложения) / Пер. с англ. Гольштейна Е. Г. и Сушкевича М. И., под ред. Юдина Д. Б. Государственное издательство физико-математической литературы, Москва, 1961 (djvu)
- ↑ 3,00 3,01 3,02 3,03 3,04 3,05 3,06 3,07 3,08 3,09 3,10 3,11 3,12 3,13 3,14 Лунгу К. Н. Линейное программирование. Руководство к решению задач. — М.: Физматлит, 2005. — 128 с. — ISBN 5-9221-0631-7.(djvu)
- ↑ 4,0 4,1 4,2 4,3 Alexander Schrijver. Combinatorial optimization. Springer-Verlag, 2003, ISBN 3-540-44389-4
- ↑ 5,0 5,1 G. Monge. Mémoire sur la théorie des déblais et des remblais. Histoire de l’Académie Royale des Sciences de Paris, avec les Mémoires de Mathématique et de Physique pour la même année, pages 666—704, 1781.
- ↑ On the history of the transportation and maximum flow problems, Alexander Schrijver, Department of Mathematics, University of Amsterdam.
- ↑ Толстой, А. Н. — «Методы нахождения наименьшего суммового километража при планировании перевозок в пространстве» — «Планирование перевозок: Сборник первый» — Транспечать НКПС (Народного комиссариата путей сообщения), Москва, 1930 г. — стр. 23—55
- ↑ Толстой А. Н., «Методы устранения нерациональных перевозок при планировании» — издание Социалистический Транспорт, выпуск 9, стр. 28—51. Повторная публикация: «Метод устранения нерациональных перевозок при составлении оперативных планов» — Трансжелдориздат, Москва, 1941 год.
- ↑ 9,0 9,1 Hitchcock F. L, Distribution of a Product from Several Sources to Numerous Localities. Journal of Mathematical Physics 20, 1941.
- ↑ 10,0 10,1 Koopmans T. С. Optimum Utilization of the Transportation System, Econometrica 17, Supplement, 1949.
- ↑ 11,0 11,1 11,2 11,3 11,4 11,5 Dantzig, G. В., Application of the Simplex Method to a Transportation Problem, chap. XXIII of // Koopmans T.C. (ed.), Activity Analysis of Production and Allocation, Cowles Commission Monograph 13, John Wiley & Sons, Inc., New York, 1951.
- ↑ 12,0 12,1 Fоrd L. R., Jr., and D. R. Fullkerson, Solving the Transportation Problem, RAND Report RM-1736, The RAND Corporation, Santa Monica, Calif., 1956.
- ↑ 13,0 13,1 13,2 Канторович Л. В., Гавурин М. К., Применение математических методов в вопросах анализа грузопотоков, Сб. ст. Проблемы повышения эффективности работы транспорта, АН СССР, 1949, стр. 110—138.
- ↑ 14,0 14,1 Канторович Л. В. Математические методы организации и планирования производства. //Применение математики в экономических исследованиях, том 2 (под ред. В. С. Немчинова), М., Соцэкгиз, 1961, 535 стр., 251—309.
- ↑ 15,0 15,1 Канторович Л. В. О перемещении масс, Докл. АН СССР 37, № 3 (1942), 227—229.
- ↑ 16,0 16,1 Dantzig G.B. Application of the simplex method to a transportation problem. // Купманс, ред. (Кооpmans Т. С., еd), Activity analysis of production and allocation. (Cowles Commission Monograph № 13), New York, Wiley, 1951, 404 pp., 359—373.
- ↑ где — запас i-го поставщика, а — потребность j-го потребителя.
- ↑ 18,0 18,1 18,2 http://www.resolventa.ru/metod/student/transproblem.htm К. Л. Самаров. Учебное пособие для студентов. Транспортная задача. Москва, СВАО, Учебный центр «Резольвента» Ошибка цитирования Неверный тег
<ref>: название «samarov» определено несколько раз для различного содержимого - ↑ 19,0 19,1 19,2 А. В. Кузнецов, Н. И. Холод, Л. С. Костевич. Руководство к решению задач по математическому программированию. Минск «Высшая школа», 1978 г.(djvu)
- ↑ 20,0 20,1 20,2 Хазанова Л. Э. Математические методы в экономике: Учебное пособие. — 3-е изд.
- ↑ 21,0 21,1 Charnes A. and W. W. Cooper, The Stepping Stone Method of Explaining Linear Programming Calculations in Transportation Problems, Management Science 1, 1954—1955.
- ↑ Окраска ячеек применена в настоящей статье для целей наглядности и рекомендована, например, Лунгу на с.91.
- ↑ Уравнение по строкам: ; Уравнение по столбцам: .
- ↑ Хотя этот случай интуитивно понятен, тем не менее, формальная математическая запись выглядит так:
- ↑ При компьютерной реализации под словом «любое» полезно подразумевать выбор из равноценных вариантов при помощи генератора случайных чисел.
- ↑ 26,0 26,1 26,2 26,3 26,4 26,5 Ф. Е. Карпелевич и Л. Е. Садовский. Элементы линейной алгебры и линейного программирования. Физматгиз, 1963. (djvu)
- ↑ 27,0 27,1 27,2 http://code.activestate.com/recipes/576575-stepping-stone-algorithum-for-solving-the-tranship/ Stepping stone algorithum for solving the transhipment problem (Python recipe). Created by James Coliins on Sat, 29 Nov 2008 (MIT). Ошибка цитирования Неверный тег
<ref>: название «python» определено несколько раз для различного содержимого - ↑ http://jean-pierre.moreau.pagesperso-orange.fr/Basic/transpor_bas.txt Modèles pratiques de décision Tome 2, By Jean-Pierre Blanger, PSI Editions, France, 1982
- ↑ http://jean-pierre.moreau.pagesperso-orange.fr/Pascal/transpor_pas.txt Modèles pratiques de décision Tome 2, By Jean-Pierre Blanger, PSI Editions, France, 1982. Pascal Release 1.0 By J-P Moreau, Paris.
- ↑ http://infostart.ru/public/89917/
- ↑ 31,0 31,1 Б.Банди «Основы линейного программирования» М:Радио и связь, 1989 (djvu)
- ↑ http://kb.mista.ru/article.php?id=859 Решение транспортной задачи в 1С:Предприятие 8.2