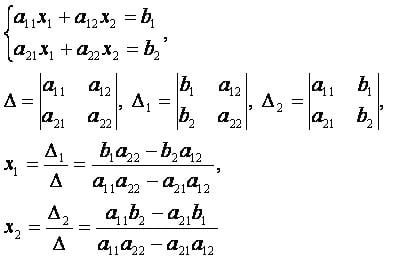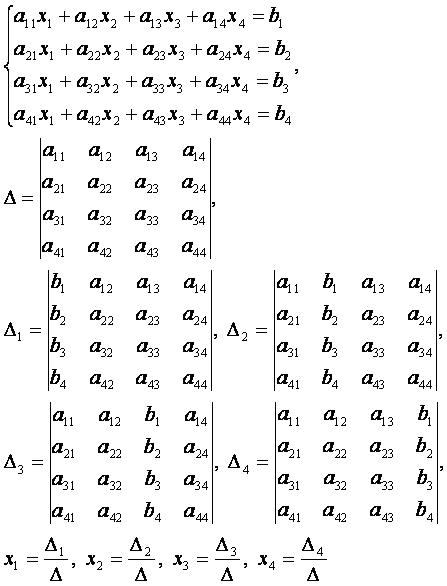Метод Крамера

Видеоурок "Метод определителей (Крамера)" // Математика от alwebra.com.ua [4:20]

Метод Крамера — это способ решения системы линейных уравнений, при котором неизвестные вычисляются в виде отношений определителей.

Описание метода

Суть метода Крамера состоит в расчёте определителей и применении формул Крамера, по которым решение x_i равно отношению i-го вспомогательного определителя Δ_i к главному Δ.

Для решения методом Крамера системы линейных уравнений вида Ax=b (где A – квадратная матрица nxn коэффициентов системы, а b – вектор свободных членов системы), сначала найдём главный определитель системы Δ. Метод Крамера применим, если главный определитель системы Δ≠0.

Формулы:

Решение системы двух уравнений с двумя неизвестными

Решение системы трёх уравнений с тремя неизвестными

Решение системы четырёх уравнений с четырьмя неизвестными

Другие методы:

• метод Крамера;
• метод обратной матрицы;
• метод неполного решения;
• метод Гаусса;
• метод простых итераций;
• метод Зейделя.

• Для решения систем нелинейных уравнений используется метод Ньютона.

Литература

• Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Наука, 1970

Ссылки

• Участник:Logic-samara