Парадоксы в теории вероятностей
Парадоксы в теории вероятностей — различного рода парадоксы, возникающие в теории вероятностей из-за несовершенства аксиоматики, в частности из-за определения вероятности через вероятность, неопределённости понятия «равновероятные события» и иных пробелов в основаниях данного раздела математики.
Основания возникновения парадоксов[править]
В теории вероятностей парадоксы бывают двух типов: первый — когда существует строгое решение в рамках аксиоматики, просто оно не очевидно, и условия задачи таковы, что ведут интуитивное понимание условий в ошибочном ключе, примерами таких парадоксов являются — Проблема Монти Холла, Санкт-Петербургский парадокс, Парадокс закона больших чисел Бернулли, Парадокс дней рождения; второй тип — парадоксы, которые основываются на неоднозначной интерпретации аксиоматики теории вероятности, её недоопределённости, которую отмечал еще Пуанкаре[1], их и можно назвать истинными парадоксами. Примеры истинных парадоксов: Парадокс двух конвертов, Парадокс Хемпеля, Парадокс Бертрана. Ценность обоих типов парадоксов в том, что они помогают лучше понять суть теории, область её ограничения, глубже понять основания теории, и иногда исследование парадоксов вело к созданию отдельных разделов математики.
Наиболее известные парадоксы[править]
Санкт-Петербургский парадокс[править]
Парадокс получил известность после публикации Даниилом Бернулли в заметках Академии наук Санкт-Петербурга в 1738 году[2], однако впервые парадокс упоминается двоюродным братом Даниила, — Николаем Бернулли в 1713 году в письме к математику Монмору[3]. Иногда, ошибочно, парадокс приписывают Эйлеру[4]. Суть парадокса: игроком бросается правильная монета до момента выпадения решки, игрок при выпадении получает рублей, где — это номер бросания, при котором выпала решка, — при каждом последующем бросании потенциальный выигрыш увеличивается вдвое. Сколько необходимо выплатить игроку за участие в игре с такими условиями, чтобы его средний выигрыш перекрыл выплату за игру. Ответ парадоксален, — математическое ожидание банковских выплат бесконечное. Выигрыш может выпасть при любом из r бросаний, тогда математическое ожидание равняется[5]:
Этот бесконечный ряд расходится, то есть имеет бесконечную сумму.
Парадокс пытались исследовать Бюффон, Крамер, однако приемлемого решения задачи в общем виде до сих пор нет, есть некоторые частные решения. например, если число бросаний ограничено 1 миллионом, банк начинает выигрывать, когда средняя ставка игрока составляет 21 рубль. Хотя Петербургский парадокс как модель используется в оценке финансовых рисков при инвестициях, она больше говорит о неопределённости финансовых рисков[2].
Сам факт, что петербургская Проблема не получила уникального и вообще приемлемого решения более, чем за 200 лет попыток крупнейшими умами мира, предполагает, что проблема роста акций не оставляет никаких надежд на удовлетворительное решение.
Дэвид Дюран, Рост акций и петербургский парадокс
Парадокс закона больших чисел Бернулли[править]
Так как по Закону больших чисел, при достаточно большом числе подбрасываний правильной монеты, частота выпадения орла и решки стремится к , то игроки считают, что чем чаще выпадает орёл, тем больше вероятность выпасть решке на каждом последующем броске и наоборот[6]. Парадокс основан на интуитивном понимании Закона больших чисел, при котором монете приписывается «память», то есть результат последующих бросаний должен зависеть от предыдущих, что, естественно, невозможно, каждое отдельное бросание независимо от предыдущих и последующих, и вероятность выпадения последовательностей ОООООООООООООР и РОРОРОРОРОРОРО (Р — решка, О — орёл) одинаковы и составляют , для правильной монеты[6].
Парадокс Монти Холла[править]
Следующая версия проблемы была изложена в журнале Parade Magazine в 1990 году, сам парадокс основан на телешоу «Let’s Make a Deal», и назван по имени ведущего этой передачи. Условие задачи следующее:
Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трех дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас, не желаете ли вы изменить свой выбор и выбрать дверь номер 2. Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
Обычно интуитивно даётся ответ , который не верен, так как при смене выбора вероятность выигрыша автомобиля увеличивается до двух третей, так как своим первоначальным выбором участник делит двери на выбранную — A и две другие — B и C, и вероятность того, что автомобиль находится за выбранной дверью = 1/3, того, что за двумя другими = 2/3, поэтому всегда выгоднее сменить выбор вопреки интуитивному пониманию[7].
В данном виде задача изложена не полно, существует стратегия «адский Монти», когда ведущий предлагает сменить выбор только тогда, когда первым ходом выбран автомобиль. Обычно задача рассматривается при следующих дополнительных условиях: автомобиль равновероятно находится за любой из дверей, ведущий в любом случае открывает одну дверь за которой находится коза и предлагает изменить выбор, если игрок выбрал автомобиль изначально, то ведущий выбирает любую из дверей за которой коза с одинаковой вероятностью.
Парадокс двух конвертов[править]
В различных формулировках парадокс известен с 1930 года, вариант с двумя конвертами, который и получил большую популярность, описан в конце 1980-х. Условия парадокса следующие — существует два конверта с деньгами, сумма в одном конверте в два раза больше суммы в другом, предлагается выбранный конверт открыть, и в случае желания выбрать другой конверт. Если в первом (открытом) конверте была сумма А, во втором может находиться 0,5•(2•А) + 0,5•(0,5•А) = 1,25•А, что больше А. При таких условиях целесообразнее отказаться от первого конверта и выбрать второй, однако, все те же рассуждения справедливы при выборе второго конверта — бóльшую привлекательность приобретает первый, и наоборот, до бесконечности[8]. Различные варианты разрешения парадокса предлагаются до сих пор[9].
В случае, если будет найдено приемлемое решение, разрешающее парадокс, это поможет найти решения в различных теоретических и прикладных областях: наглядное понимание некоторых парадоксов термодинамики, оптимизация работы технических систем, улучшение электронных схем, составление выигрышной стратегии игры на фондовом рынке[8].
Ключом к пониманию парадокса служит рассмотрение двух задач, где задача А - количество денег в конверте никогда не может превышать Х единиц. В данном случае, открыв конверт с деньгами и получив чек на более чем Х/2 единиц денег, игрок заведомо осведомлен, что его конверт больший. Задача В - количество денег в большем конверте равно от 2 единиц до бесконечности, так же сводится к задачам С и D. С - когда игрок получает 1 единицу денег и знает, что его конверт меньший. В случае задачи D мы имеем ситуацию, в которой математическое ожидание количества денег, лежащих в конверте полученных игроком, равно ∞/2 и при обмене конверта математическое ожидание его выигрыша равно 1,25•∞/2. Учитывая равенство ∞/2 и 1,25•∞/2, можно прийти к выводу, что с вероятностью 1 - 1/∞ наступит ситуация, когда обмен безразличен. Таким образом, если не рассматривать ситуации С и D, то нужно сделать замечание, что в области действительных чисел возможна экспертная оценка возможности выигрыша и проигрыша.
Парадокс Бертрана[править]
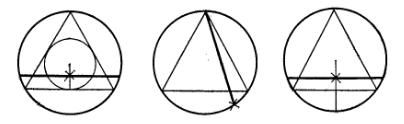
Парадокс был описан в работе Ж. Бертрана «Исчисление вероятностей» (Calcul des probabilites) 1898 года. Суть парадокса: для произвольной окружности произвольно выбирается хорда, какова вероятность того, что она длиннее стороны равностороннего треугольника. Изначально было предложено три метода:
- Случайным образом в круге выбирается точка, она определяет единственную хорду, серединой которой является (за исключением центра, но в этом случае все хорды эквивалентны), в этом случае хорда длиннее стороны треугольника, когда эта точка лежит во вписанном круге с радиусом в половину первого круга и с тем же центром. Вероятность попадания произвольной точки в этот круг — отношение площадей меньшего и большего кругов и составляет .
- Если случайным образом на окружности выбирается точка, служащая одним концом хорды, и одновременно является углом треугольника, то хорда будет длиннее стороны треугольника только в случае если она пересекает противоположную углу сторону. Вероятность этого определяется длинами дуг отсекаемых каждой стороной, их три и они равны между собой — то есть вероятность события .
- В случае, если на радиусе произвольно выбирается точка, и хорда проводится перпендикулярно радиусу в этой точке, то так как сторона треугольника делит перпендикулярный ей радиус пополам, то вероятность события — .
При разных изначальных предположениях об исходных равновероятных событиях, можно получить любой желаемый результат, от единицы до — например, в случае если радиус произвольной окружности изменяется от бесконечной длины до конечной, соответственно, а хорда получается сечением окружности произвольной прямой на бесконечной плоскости. Данный парадокс дал начало новому разделу математики — интегральной геометрии, которая позволяет реконструировать исходные объекты по их сечениям или проекциям, что находит применение в минералогии, металлургии, биологии и медицины — при реконструкции данных томографии[10].
Парадокс второго ребёнка (парадокс мальчика и девочки)[править]
Парадокс сформулирован в 1959-ом году Мартином Гарднером в статье «The Two Children Problem» опубликованной в журнале Scientific American. Первая формулировка была следующей:
У мистера Джонса двое детей. При этом старший ребенок - девочка. Какова вероятность того, что оба ребенка девочки? У мистера Смита двое детей. При этом хотя бы один ребенок – мальчик. Какова вероятность того, что оба ребенка мальчики?
Интуитивный вариант на второй вопрос это что вероятность равна , хотя на самом деле поле равновероятных событий в этом случае состоит из трёх вариантов — ММ, МД, ДМ (если дети не близнецы), и вариант ММ только один из них, следовательно, искомая вероятность равна . Сам Гарднер впоследствии понял, что в третьем варианте ситуация неоднозначна, и зависит от дополнительных условий - в зависимости от того, при каких условиях выясняется, что второй ребёнок мальчик[11].
См. также[править]
Источники[править]
- ↑ А именно нечётком определении равновероятных событий. А. Пуанкаре, «О науке»; «Исчисление вероятностей», Париж. 1912 год.
- ↑ 2,0 2,1 Инвесто.ру, перевод статьи Two Lessons from the St. Petersburg Paradox
- ↑ Г. Секкей, 35 стр.
- ↑ Константин Яблочкин, Санкт-Петербургский парадокс
- ↑ Г. Секкей, 36 стр.
- ↑ 6,0 6,1 ПАРАДОКС ЛОТЕРЕИ И ЗАКОНА БОЛЬШИХ ЧИСЕЛ БЕРНУЛЛИ
- ↑ Сергей Вальковский, Задача Монти Холла
- ↑ 8,0 8,1 http://www.membrana.ru/particle/2349
- ↑ Найдено оригинальное решение парадокса двух конвертов
- ↑ Г. Секкей, стр. 50-54
- ↑ The Second Scientific American Book of Mathematical Puzzles and Diversions. — Simon & Schuster, 1961. — ISBN 978-0226282534..
Литература[править]
- Г. Секкей, «Парадоксы в теории вероятностей и математической статистике» М., Мир 1990
- М. Гарднер «Гексафлексагоны и Другие Математические Развлечения»