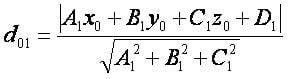Расстояние от точки до плоскости в трёхмерном пространстве

Видеоурок «Расстояние от точки до плоскости» // Математика от alwebra.com.ua [5:29]

§44 Расстояние от точки до плоскости // Мемория Высшая Математика [8:16]

Формула расстояния от точки до плоскости в координатной форме

Расстояние от точки до плоскости — это длина перпендикуляра к плоскости, опущенного из точки.

Обозначения

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar r_0=(x_0,y_0,z_0)} — радиус-вектор точки;

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar n_1=(A_1,B_1,C_1)} — нормаль к плоскости;

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A_1x+B_1y+C_1z+D_1=0} — уравнение плоскости;

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle d_{01}} — расстояние от точки до плоскости.

Формулы

Векторная форма

Для точки и плоскости формула расстояния имеет вид:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle d_{01}=\frac{\left|\left(\bar r_0\cdot \bar n_1\right)+D_1\right|}{\left|\bar n_1\right|}}

Расстояние от точки до плоскости равно отношению модуля суммы скалярного произведения векторов (r₀ и n₁) и коэффициента D₁ к длине нормали (n₁). Геометрический смысл формулы: расстояние - это длина отклонения точки от плоскости.

Координатная форма

Формула расстояния от точки до плоскости в координатной форме имеет вид:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle d_{01}=\frac{\left|A_1x_0+B_1y_0+C_1z_0+D_1\right|}{\sqrt{A_1^2+B_1^2+C_1^2}}}

Пример

Даны точка и плоскость: Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (-4;3;5)} и Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -x+2y-2z+9=0} .

Найти расстояние между ними.

Решение.

Дана точка Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (-4;3;5)\Rightarrow\bar r_0=(-4;3;5)}

Дана плоскость Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -x+2y-2z+9=0\Rightarrow\bar n_1=(-1;2;-2),\ D_1=9}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left(\bar r_0\cdot\bar n_1\right)=\left((-4;3;5)\cdot(-1;2;-2)\right)=(-4)\cdot(-1)+3\cdot 2+5\cdot(-2)=0}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left|\bar n_1\right|=\left|(-1;2;-2)\right|=\sqrt{(-1)^2+2^2+(-2)^2}=\sqrt{1+4+4}=\sqrt{9}=3}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle d_{01}=\frac{\left|\left(\bar r_0\cdot\bar n_1\right)+D_1\right|}{\left|\bar n_1\right|}=\frac{|0+9|}{3}=3}

Другие формулы:

1. расстояние между точками;
2. расстояние между прямыми;
3. расстояние от точки до прямой;
4. расстояние от точки до плоскости.

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970