Скалярное произведение

Скалярное произведение векторов [14:19]

9 класс, 18 урок, Скалярное произведение векторов // Видеокурсы DA VINCI [7:04]

Скалярное произведение векторов — число, равное сумме произведений координат двух векторов-сомножителей.

Также скалярное произведение векторов можно равносильно определить как произведение модулей на косинус угла между ними. В школе такое определение является достаточно традиционным, если вообще не самым частым.

Почему именно косинус

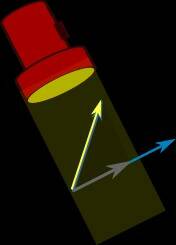
Для того, чтобы это было понятно, желательно дать другое определение скалярного произведения, которое, наверное, было бы самым по-человечески интуитивным: скалярное произведение векторов — это произведение модуля первого вектора и проекции второго на первый. Такое определение обычно можно встретить только вне школьной базовой программы, — например, в вузах, а также просто в специализированной литературе.

По этому определению смысл скалярного умножения оказывается очень прост: скалярное произведение — мера того, насколько векторы, с одной стороны, длинны сами по себе, а с другой стороны, насколько они сонаправлены друг другу. Если проекция одного вектора на второй сонаправленна этому второму вектору, скалярное произведение будет положительным; если противонаправленна — отрицательным.

Данное определение очень полезно не только само по себе, но и тем, что именно благодаря нему некоторые из свойств скалярного произведения становятся в разы прозрачнее, чем по определениям из преамбулы.

Обозначения

r₁ = (x₁, y₁, z₁) — первый вектор;

r₂ = (x₂, y₂, z₂) — второй вектор;

Обычно скалярное произведение векторов a и b обозначается через точку:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathbf a\cdot\mathbf b}

или, что более редко, в круглых скобках:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (\mathbf a, \mathbf b).}

Формула

Для трёхмерного пространства:

(r₁ ∙ r₂) = (x₁ x₂ + y₁ y₂ + z₁ z₂)

Через косинус:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathbf r_1 \cdot \mathbf r_2 = r_1r_2\cos\widehat{\mathbf r_1 \mathbf r_2}.}

По координатам:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (a_1, a_2,\ ..., a_n) \cdot (b_1,\ ..., b_n) = a_1b_1 \, + \, ... + \, a_nb_n.}

Через проекции:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathbf r_1 \cdot \mathbf r_2 = r_1\cdot(r_2)_{\parallel\mathbf r_1} = (r_1)_{\parallel\mathbf r_2} \cdot r_2.}

Свойства

Переместительное свойство:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathbf r_1 \cdot \mathbf r_2 = \mathbf r_2 \cdot \mathbf r_1.}

Два свойства линейности:

• Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (\mathbf r_1 + \mathbf r_2) \cdot \mathbf r_3 = \mathbf r_1 \cdot \mathbf r_3 + \mathbf r_2 \cdot \mathbf r_3, \qquad \mathbf r_1 \cdot (\mathbf r_2 + \mathbf r_3) = \mathbf r_1 \cdot \mathbf r_2 + \mathbf r_1 \cdot \mathbf r_3;}
• Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (a_1 \mathbf r_1) \cdot (a_2 \mathbf r_2) = a_1a_2(\mathbf r_1 \cdot \mathbf r_2).}

Скалярный квадрат:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (a_1,\ ..., a_n) \cdot (a_1,\ ..., a_n) = |(a_1,\ ..., a_n)|^2 = a_1^2 \, + \, ... + \, a_n^2.}

Умножение на нулевой вектор:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathbf{r \cdot 0} = \mathbf{0 \cdot r} = \mathbf0.}

Распределительное свойство

Отдельного внимания, пожалуй, заслуживает распределительное свойство, или дистрибутивность, скалярного умножения относительно сложения. Дело в том, что доказательство — да и вообще само реальное понимание причины этого свойства возникает именно при использовании определения через проекцию, так как в таком случае теорема оказывается очень очевидной:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (\mathbf r_1 + \mathbf r_2) \cdot \mathbf r_3 = \big(\text{proj}_{\mathbf r_3}(\mathbf r_1 + \mathbf r_2)\big)r_3 = (\text{proj}_{\mathbf r_3}\mathbf r_1 + \text{proj}_{\mathbf r_3}\mathbf r_2)r_3 = \mathbf r_1 \cdot \mathbf r_3 + \mathbf r_2 \cdot \mathbf r_3,}

если конец первого слагаемого внутри скобки совместить с началом второго слагаемого.

Равносильность определений

Если между определениями через проекцию и через косинус равносильность довольно ясна, то их равносильность по отношению к координатному определению не очень очевидна. Для того, чтобы это «прочувстовать», можно использовать доказательство с использованием дистрибутивности (которую, в свою очередь, мы выше доказали с помощью определения через те самые проекции):

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{align} (a_1\mathbf i_1 \, + \, ... + \, a_n\mathbf i_n) \cdot (b_1\mathbf i_1 \, + \, ... + \, b_n\mathbf i_n) & = a_1\mathbf i_1\cdot(b_1\mathbf i_1 \, + \, ... + \, b_n\mathbf i_n) \, + \\ & + a_2\mathbf i_2\cdot(b_1\mathbf i_1 \, + \, ... + \, b_n\mathbf i_n) \, + \\ & + \, ... + \\ & + a_n\mathbf i_n \cdot(b_1\mathbf i_1 \, + \, ... + \, b_n\mathbf i_n) = \\ & = a_1b_1 + \\ & + \, ... + \\ & \, + a_nb_n. \end{align}}

Интеграл по кривой

Есть два вида криволинейных интеграла:

1. где функция интегрируется по обычной кривой;
2. где функция интегрируется по ориентированной кривой.

Во втором случае обычно в качестве функции используют векторное поле F(r) — и тогда, как правило, функцию F(r) и бесконечно малый вектор dr, сонаправленный ориентированной кривой, связывают именно скалярным произведением:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \int_{\vec C}\mathbf F(\mathbf r)\cdot\text{d}\mathbf r.}

Тогда интеграл называется криволинейным интегралом второго рода.

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970

Другие операции

1. нахождение длины вектора;
2. сложение векторов;
3. вычитание векторов;
4. умножение вектора на число;
5. умножение координат векторов;
6. деление координат векторов;
7. извлечение корня из координат вектора;
8. скалярное произведение;
9. векторное произведение;
10. смешанное произведение;
11. двойное векторное произведение;
12. нахождение угла между векторами;
13. проекция вектора на вектор;
14. ортогонализация векторов.