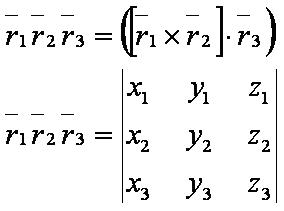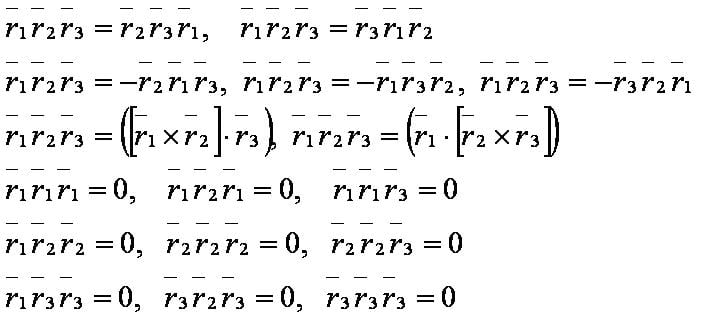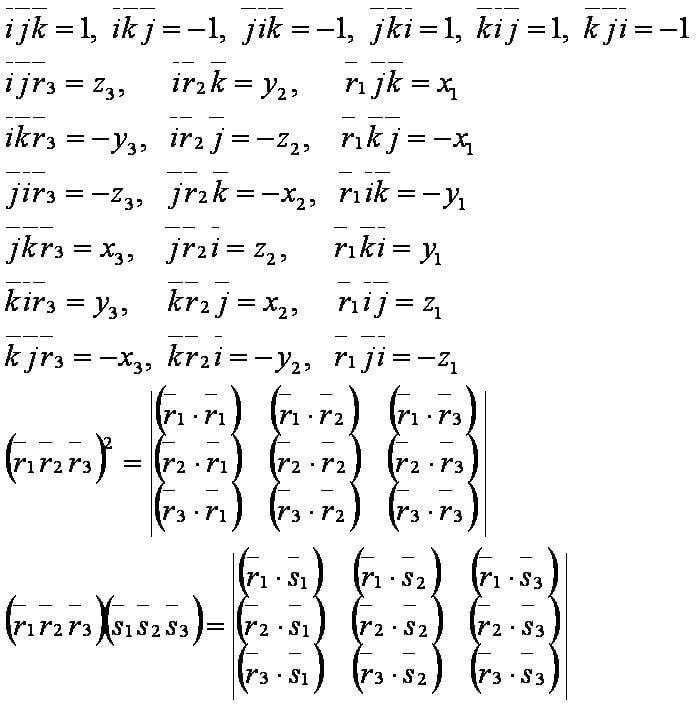Смешанное произведение
Перейти к навигации
Перейти к поиску
Смешанное произведение векторов — число, равное векторно-скалярному произведению трёх векторов, т.е. сначала берётся векторное произведение первых двух векторов, а затем — скалярное произведение полученного вектора и третьего вектора.
Геометрический смысл смешанного произведения трёх векторов — объём параллелепипеда, построенного на этих векторах, взятый со знаком "+", если эти векторы образуют правую тройку, и со знаком "-", если эти векторы образуют левую тройку.
Обозначения[править]
r1 = (x1, y1, z1) — первый вектор;
r2 = (x2, y2, z2) — второй вектор;
r3 = (x3, y3, z3) — третий вектор.
Формула[править]
Свойства[править]
Литература[править]
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970
Ссылки[править]
- временные ссылки
Другие операции[править]
- нахождение длины вектора;
- сложение векторов;
- вычитание векторов;
- умножение вектора на число;
- умножение координат векторов;
- деление координат векторов;
- извлечение корня из координат вектора;
- скалярное произведение;
- векторное произведение;
- смешанное произведение;
- двойное векторное произведение;
- нахождение угла между векторами;
- проекция вектора на вектор;
- ортогонализация векторов.