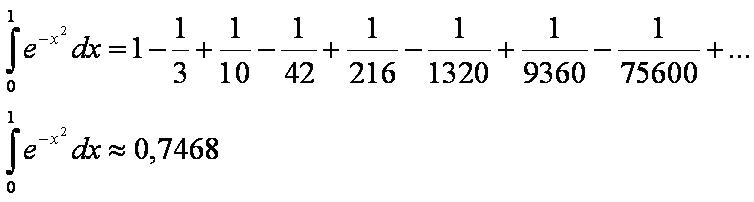Интеграл Эйлера — Пуассона
(перенаправлено с «Интеграл Эйлера-Пуассона»)
Перейти к навигации
Перейти к поиску
Интеграл Эйлера — Пуассона — определенный интеграл вида:
Вывод формулы[править]
Следствие[править]
Дополнение[править]
Для фиксированного x имеем:
При x = 1 получаем:
Другие интегралы:[править]
- интеграл;
- интегралы элементарных функций;
- интегралы дробно-рациональных функций;
- интегралы функций с корнями;
- интегралы тригонометрических функций;
- интегралы обратных тригонометрических функций;
- интегралы гиперболических функций;
- интегралы обратных гиперболических функций;
- интеграл Фурье;
- интеграл Фурье комплексный;
- эллиптические интегралы;
- интегралы, определяемые методом замены переменных;
- интегралы, определяемые по интегральным равенствам;
- интегралы, определяемые по интегральным формулам;
- интеграл Эйлера-Пуассона.
Литература[править]
- Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики — М.: «Наука», 1975.

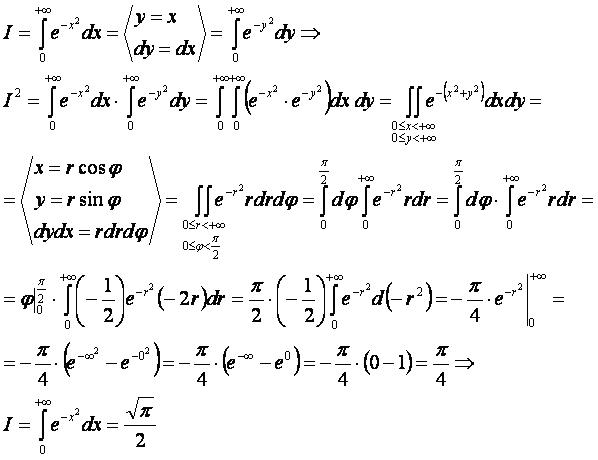

![{\displaystyle \int \limits _{0}^{x}e^{-t^{2}}dt=\int \limits _{0}^{x}\left[\sum \limits _{n=0}^{\infty }{\frac {(-1)^{n}t^{2n}}{n!}}\right]dt=\sum \limits _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{n!(2n+1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b17c7e288654ed031c4d1b4c02875adaaff7e7d1)