Производственная задача

Математическая модель ПЗ

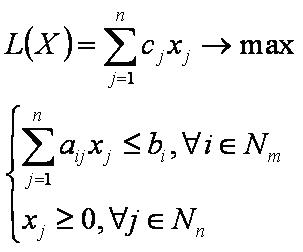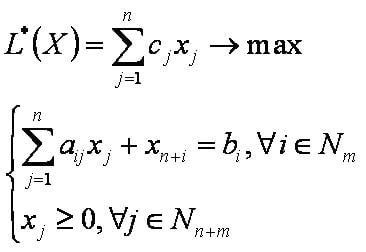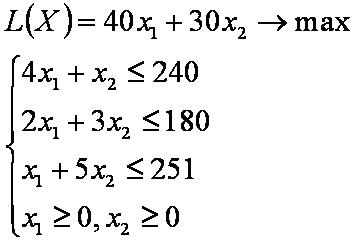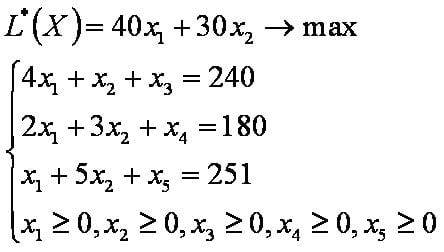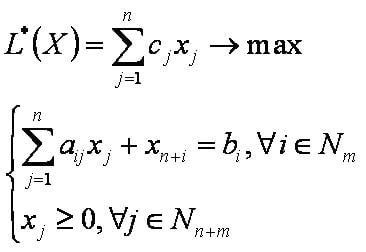
Математическая модель эквивалентной ПЗ

Производственная задача — задача линейного программирования: определение плана производства изделий с максимальной стоимостью при заданных ограничениях по объемам ресурсов.

Постановка задачи

Имеется n видов изделий и m видов ресурсов. Пусть заданы нормы a_ij расхода i-го ресурса на производство j-го изделия и объёмы b_i запасов i-го ресурса, i=1,2,…,m, j=1,2,…,n. Пусть известна для j-го изделия цена c_j, j=1,2,…,n. Необходимо определить план производства изделий с максимальной стоимостью. Производственная задача (ПЗ) формулируется следующим образом:

$L(X)=\sum \limits _{j=1}^{n}c_{j}x_{j}\rightarrow \max$

${\begin{cases}\sum \limits _{j=1}^{n}a_{ij}x_{j}\leq b_{i},\ \forall i\in N_{m}\\x_{j}\geq 0,\forall j\in N_{n}\end{cases}}$

или

$L(X)=c_{1}x_{1}+c_{2}x_{2}+\ldots +c_{n}x_{n}\rightarrow \max$

${\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}\leq b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}\leq b_{2}\\\ldots \\a_{m1}x_{1}+a_{m2}x_{2}+\ldots +a_{mn}x_{n}\leq b_{m}\\x_{1}\geq 0,\ x_{2}\geq 0,\ldots ,\ x_{n}\geq 0\end{cases}}$

где x_j — объём выпуска j-го изделия, j=1,2,…,n.

Постановка эквивалентной задачи

Для решения производственной задачи необходимо иметь ограничения в форме равенств. Введём новые переменные x_j – остатки неиспользуемых ресурсов (j-n)-го вида, j=n+1,n+2,…,n+m. Добавим эти переменные к соответствующим ограничениям, и в результате получим эквивалентную задачу.

Математическая модель эквивалентной задачи принимает следующий вид:

$L^{+}(X)=\sum \limits _{j=1}^{n}c_{j}x_{j}\rightarrow \max$

${\begin{cases}\sum \limits _{j=1}^{n}a_{ij}x_{j}+x_{n+i}=b_{i},\ \forall i\in N_{m}\\x_{j}\geq 0,\forall j\in N_{n+m}\end{cases}}$

или

$L^{+}(X)=c_{1}x_{1}+c_{2}x_{2}+\ldots +c_{n}x_{n}\rightarrow \max$

${\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}+x_{n+1}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}+x_{n+2}=b_{2}\\\ldots \\a_{m1}x_{1}+a_{m2}x_{2}+\ldots +a_{mn}x_{n}+x_{n+m}=b_{m}\\x_{1}\geq 0,\ x_{2}\geq 0,\ldots ,\ x_{n+m}\geq 0\end{cases}}$

Метод решения

Эквивалентная производственная задача решается симплекс-методом.

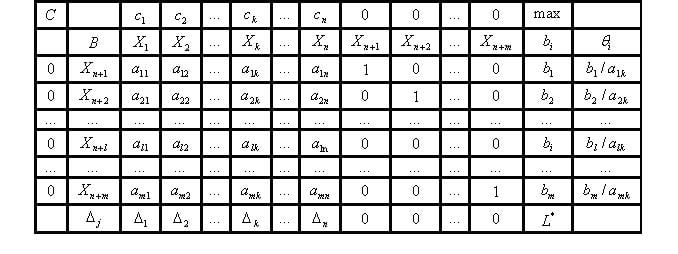
Начальная симплекс-таблица для эквивалентной задачи имеет вид:

Пример решения

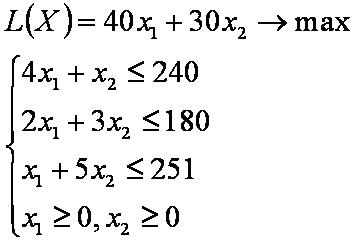
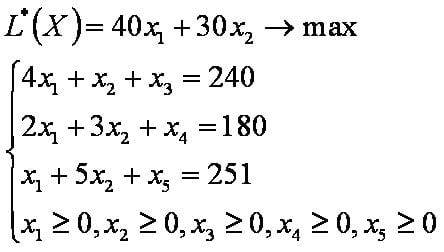
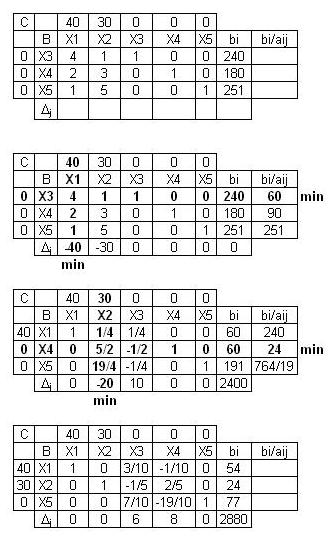
Оптимальное решение эквивалентной задачи x₁=54, x₂=24, x₃=0, x₄=0, x₅=77, L*=2880.

Оптимальное решение производственной задачи x₁=54, x₂=24, L=2880.

Другие задачи:

• Каноническая задача;
• Производственная задача;
• Общая прямая задача линейного программирования;
• Общая двойственная задача линейного программирования;
• Задачи транспортного типа;
• Задача целочисленного программирования;
• Задача о рюкзаке;
• Задача распределения средств;
• Задача замены оборудования.

Литература

• Юдин Д. Б., Гольштейн Е. Г. Линейное программирование., М.,1963.

Ссылки

• Участник:Logic-samara