VIDEO
Расстояние от точки до прямой в пространстве [1:09]
VIDEO
Расстояние от точки до прямой (метод координат) [5:40]
Формула расстояния от точки до прямой в координатной форме
Расстояние от точки до прямой — это длина перпендикуляра к прямой, опущенного из точки.
r
¯
0
=
(
x
0
,
y
0
,
z
0
)
{\displaystyle {\bar {r}}_{0}=(x_{0},y_{0},z_{0})}
вектор точки;
r
¯
1
=
(
x
1
,
y
1
,
z
1
)
{\displaystyle {\bar {r}}_{1}=(x_{1},y_{1},z_{1})}
s
¯
1
=
(
l
1
,
m
1
,
n
1
)
{\displaystyle {\bar {s}}_{1}=(l_{1},m_{1},n_{1})}
x
−
x
1
l
1
=
y
−
y
1
m
1
=
z
−
z
1
n
1
{\displaystyle {\frac {x-x_{1}}{l_{1}}}={\frac {y-y_{1}}{m_{1}}}={\frac {z-z_{1}}{n_{1}}}}
d
01
{\displaystyle d_{01}}
Векторная форма [ править ] Для точки и прямой формула расстояния имеет вид:
d
01
=
|
[
(
r
¯
0
−
r
¯
1
)
×
s
¯
1
]
|
|
s
¯
1
|
⇔
d
01
=
S
(
r
¯
0
−
r
¯
1
)
s
¯
1
|
s
¯
1
|
{\displaystyle d_{01}={\frac {\left|\left[\left({\bar {r}}_{0}-{\bar {r}}_{1}\right)\times {\bar {s}}_{1}\right]\right|}{\left|{\bar {s}}_{1}\right|}}\Leftrightarrow d_{01}={\frac {S_{\left({\bar {r}}_{0}-{\bar {r}}_{1}\right){\bar {s}}_{1}}}{\left|{\bar {s}}_{1}\right|}}}
Расстояние от точки до прямой равно отношению модуля векторного произведения векторов (r0 − r1 ) s1 к длине вектора s1 .
Геометрический смысл формулы: расстояние — это длина высоты параллелограмма (построенного на векторах (r0 − r1 ) s1 ), опущенной на основание параллелограмма в виде вектора (s1 ), равная отношению площади параллелограмма к длине основания.
Координатная форма [ править ] Формула расстояния от точки до прямой в координатной форме имеет вид:
d
01
=
|
x
0
−
x
1
y
0
−
y
1
l
1
m
1
|
2
+
|
y
0
−
y
1
z
0
−
z
1
m
1
n
1
|
2
+
|
z
0
−
z
1
x
0
−
x
1
n
1
l
1
|
2
l
1
2
+
m
1
2
+
n
1
2
{\displaystyle d_{01}={\frac {\sqrt {{\begin{vmatrix}x_{0}-x_{1}&y_{0}-y_{1}\\l_{1}&m_{1}\end{vmatrix}}^{2}+{\begin{vmatrix}y_{0}-y_{1}&z_{0}-z_{1}\\m_{1}&n_{1}\end{vmatrix}}^{2}+{\begin{vmatrix}z_{0}-z_{1}&x_{0}-x_{1}\\n_{1}&l_{1}\end{vmatrix}}^{2}}}{\sqrt {l_{1}^{2}+m_{1}^{2}+n_{1}^{2}}}}}
Даны точка и прямая:
(
−
4
;
3
;
5
)
{\displaystyle (-4;3;5)}
x
−
1
−
2
=
y
+
5
3
=
z
+
1
4
{\displaystyle {\frac {x-1}{-2}}={\frac {y+5}{3}}={\frac {z+1}{4}}}
Найти расстояние между ними.
Решение.
Дана точка
(
−
4
;
3
;
5
)
⇒
r
¯
0
=
(
−
4
;
3
;
5
)
{\displaystyle (-4;3;5)\Rightarrow {\bar {r}}_{0}=(-4;3;5)}
Дана прямая
x
−
1
−
2
=
y
+
5
3
=
z
+
1
4
⇒
r
¯
1
=
(
1
;
−
5
;
−
1
)
,
s
¯
1
=
(
−
2
;
3
;
4
)
{\displaystyle {\frac {x-1}{-2}}={\frac {y+5}{3}}={\frac {z+1}{4}}\Rightarrow {\bar {r}}_{1}=(1;-5;-1),\ {\bar {s}}_{1}=(-2;3;4)}
r
¯
0
−
r
¯
1
=
(
−
4
;
3
;
5
)
−
(
1
;
−
5
;
−
1
)
=
(
−
5
;
8
;
6
)
{\displaystyle {\bar {r}}_{0}-{\bar {r}}_{1}=(-4;3;5)-(1;-5;-1)=(-5;8;6)}
[
(
r
¯
0
−
r
¯
1
)
×
s
¯
1
]
=
[
(
−
5
;
8
;
6
)
×
(
−
2
;
3
;
4
)
]
=
|
i
¯
j
¯
k
¯
−
5
8
6
−
2
3
4
|
==
14
i
¯
+
8
j
¯
+
k
¯
=
(
14
;
8
;
1
)
{\displaystyle \left[\left({\bar {r}}_{0}-{\bar {r}}_{1}\right)\times {\bar {s}}_{1}\right]=\left[(-5;8;6)\times (-2;3;4)\right]={\begin{vmatrix}{\bar {i}}&{\bar {j}}&{\bar {k}}\\-5&8&6\\-2&3&4\end{vmatrix}}==14{\bar {i}}+8{\bar {j}}+{\bar {k}}=(14;8;1)}
|
[
(
r
¯
0
−
r
¯
1
)
×
s
¯
1
]
|
=
|
(
14
;
8
;
1
)
|
=
14
2
+
8
2
+
1
2
=
196
+
64
+
1
=
261
{\displaystyle \left|\left[\left({\bar {r}}_{0}-{\bar {r}}_{1}\right)\times {\bar {s}}_{1}\right]\right|=\left|(14;8;1)\right|={\sqrt {14^{2}+8^{2}+1^{2}}}={\sqrt {196+64+1}}={\sqrt {261}}}
|
s
¯
1
|
=
|
(
−
2
;
3
;
4
)
|
=
(
−
2
)
2
+
3
2
+
4
2
=
4
+
9
+
16
=
29
{\displaystyle \left|{\bar {s}}_{1}\right|=\left|(-2;3;4)\right|={\sqrt {(-2)^{2}+3^{2}+4^{2}}}={\sqrt {4+9+16}}={\sqrt {29}}}
d
01
=
|
[
(
r
¯
0
−
r
¯
1
)
×
s
¯
1
]
|
|
s
¯
1
|
=
261
29
=
261
29
=
9
=
3
{\displaystyle d_{01}={\frac {\left|\left[\left({\bar {r}}_{0}-{\bar {r}}_{1}\right)\times {\bar {s}}_{1}\right]\right|}{\left|{\bar {s}}_{1}\right|}}={\frac {\sqrt {261}}{\sqrt {29}}}={\sqrt {\frac {261}{29}}}={\sqrt {9}}=3}
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970. 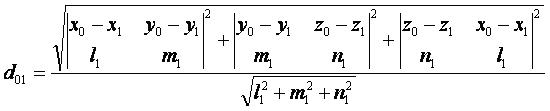





![{\displaystyle d_{01}={\frac {\left|\left[\left({\bar {r}}_{0}-{\bar {r}}_{1}\right)\times {\bar {s}}_{1}\right]\right|}{\left|{\bar {s}}_{1}\right|}}\Leftrightarrow d_{01}={\frac {S_{\left({\bar {r}}_{0}-{\bar {r}}_{1}\right){\bar {s}}_{1}}}{\left|{\bar {s}}_{1}\right|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f29704b45afafbc1c1ee2ced52e51c438c27618f)






![{\displaystyle \left[\left({\bar {r}}_{0}-{\bar {r}}_{1}\right)\times {\bar {s}}_{1}\right]=\left[(-5;8;6)\times (-2;3;4)\right]={\begin{vmatrix}{\bar {i}}&{\bar {j}}&{\bar {k}}\\-5&8&6\\-2&3&4\end{vmatrix}}==14{\bar {i}}+8{\bar {j}}+{\bar {k}}=(14;8;1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/896c98334af8636c46206cd110cf2fde4337a9ea)
![{\displaystyle \left|\left[\left({\bar {r}}_{0}-{\bar {r}}_{1}\right)\times {\bar {s}}_{1}\right]\right|=\left|(14;8;1)\right|={\sqrt {14^{2}+8^{2}+1^{2}}}={\sqrt {196+64+1}}={\sqrt {261}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9c176639d654fbf497932e8e9e081bad5eb8e19)

![{\displaystyle d_{01}={\frac {\left|\left[\left({\bar {r}}_{0}-{\bar {r}}_{1}\right)\times {\bar {s}}_{1}\right]\right|}{\left|{\bar {s}}_{1}\right|}}={\frac {\sqrt {261}}{\sqrt {29}}}={\sqrt {\frac {261}{29}}}={\sqrt {9}}=3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1097353c4da5edab6dde4d92efb833ccf4dd71b4)