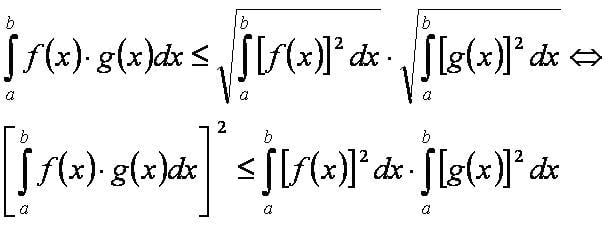Интегральное неравенство Коши-Буняковского

Интегральное неравенство Коши-Буняковского — неравенство, гласящее, что модуль определённого интеграла от произведения двух функций не превышает произведения корней из определённых интегралов от квадратов этих функций.

Формула неравенства

$\left|\int \limits _{a}^{b}f(x)\cdot g(x)dx\right|\leqslant {\sqrt {\int \limits _{a}^{b}(f(x))^{2}dx}}\cdot {\sqrt {\int \limits _{a}^{b}(g(x))^{2}dx}}\ \Leftrightarrow$

$\Leftrightarrow \left(\int \limits _{a}^{b}f(x)\cdot g(x)dx\right)^{2}\leqslant \int \limits _{a}^{b}(f(x))^{2}dx\cdot \int \limits _{a}^{b}(g(x))^{2}dx$

Пример

Применение неравенства для оценки интеграла

$\int \limits _{0}^{1}{\sqrt {1+x^{2}}}dx=\int \limits _{0}^{1}1\cdot {\sqrt {1+x^{2}}}dx\leq {\sqrt {\int \limits _{0}^{1}1^{2}dx}}\cdot {\sqrt {\int \limits _{0}^{1}\left({\sqrt {1+x^{2}}}\right)^{2}dx}}\ \Leftrightarrow$

$\Leftrightarrow \left.{\sqrt {x}}\right|_{0}^{1}\cdot {\sqrt {\int \limits _{0}^{1}\left(1+x^{2}\right)dx}}={\sqrt {1}}\cdot \left.{\sqrt {x+{\frac {x^{3}}{3}}}}\right|_{0}^{1}={\sqrt {1+{\frac {1^{3}}{3}}}}={\sqrt {\frac {4}{3}}}={\frac {2{\sqrt {3}}}{3}}$

$\Rightarrow \int \limits _{0}^{1}{\sqrt {1+x^{2}}}dx\leq {\frac {2{\sqrt {3}}}{3}}$

Другие неравенства:

• неравенство Коши;
• неравенство Коши-Буняковского;
• интегральное неравенство Коши-Буняковского;
• неравенство Минковского;
• интегральное неравенство Минковского;
• неравенство Гёльдера;
• интегральное неравенство Гёльдера;
• неравенство Маркова;
• неравенство Чебышёва.

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970.
• Выгодский М. Я. Справочник по высшей математике — М.: 1964.