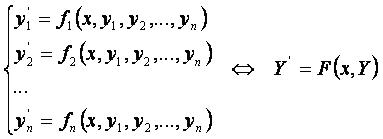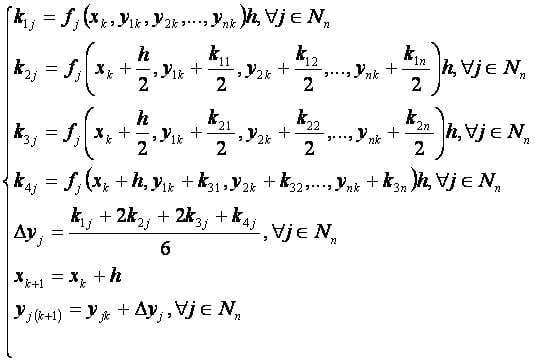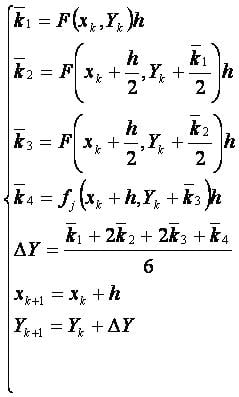Обобщённый метод Рунге-Кутты
Перейти к навигации
Перейти к поиску
Обобщённый метод Рунге-Кутты — это численный метод получения решения системы дифференциальных уравнений. Этот метод является обобщением классического метода Рунге-Кутты 4-го порядка для решения одного дифференциального уравнения.
Описание метода[править]
Суть обобщённого метода Рунге-Кутты в пошаговом вычислении значений решения Y=Y(x) системы дифференциальных уравнений вида
с начальным условием
Формулы[править]
или 
Другие методы:[править]
- метод Эйлера;
- исправленный метод Эйлера;
- усовершенствованный метод Эйлера;
- метод Адамса третьего порядка;
- метод Рунге-Кутты третьего порядка;
- классический метод Рунге-Кутты.
- Для решения систем дифференциальных уравнений используется обобщённый метод Рунге-Кутты.
Литература[править]
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
