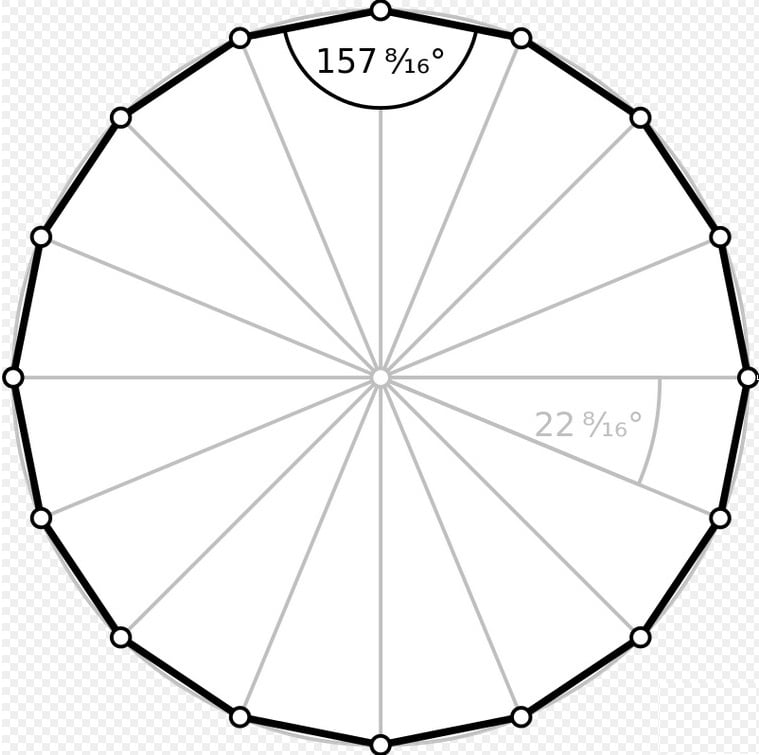
Площадь правильного шестнадцатиугольника

Правильный шестнадцатиугольник

Площадь правильного шестнадцатиугольника — число, характеризующее правильный шестнадцатиугольник в единицах измерения площади.

Определение

Правильный шестнадцатиугольник — шестнадцатиугольник (гексадекагон) у которого все стороны и углы равны.

Обозначения

a — длина стороны;

n — число сторон, n=16;

r — радиус вписанной окружности;

R — радиус описанной окружности;

α — половинный центральный угол, α=π/16=11 1/4 °;

β — внутренний угол между соседними сторонами, β=7π/8=157 1/2 °;

γ — центральный угол, γ=π/8=22 1/2 °;

P₁₆ — периметр правильного шестнадцатиугольника;

S_Δ — площадь равнобедренного треугольника с основанием, равным стороне, и боковыми сторонами, равными радиусу описанной окружности;

S₁₆ — площадь правильного шестнадцатиугольника.

Формулы

• Применяя формулу площади правильного n-угольника для n=16, получим:

$S_{16}=4a^{2}ctg{\frac {\pi }{16}}\Leftrightarrow$

$\Leftrightarrow S_{16}=16S_{\triangle },\ S_{\triangle }={\frac {a^{2}}{4}}ctg{\frac {\pi }{16}}\Leftrightarrow$

$\Leftrightarrow S_{16}={\frac {1}{2}}P_{16}r,\ P_{16}=16a,\ r={\frac {a}{2}}ctg{\frac {\pi }{16}}\Leftrightarrow$

$\Leftrightarrow S_{16}=16R^{2}\sin {\frac {\pi }{16}}\cos {\frac {\pi }{16}},\ R={\frac {a}{2\sin {\frac {\pi }{16}}}}\Leftrightarrow$

$\Leftrightarrow S_{16}=16r^{2}tg{\frac {\pi }{16}},\ r=R\cos {\frac {\pi }{16}}$

• Учитывая значения тригонометрических функций для α=π/16, получим:

$S_{16}=4\left({\sqrt {4+2{\sqrt {2}}}}+{\sqrt {2}}+1\right)a^{2}\Leftrightarrow$

$\Leftrightarrow S_{16}=16S_{\triangle },\ S_{\triangle }={\frac {{\sqrt {4+2{\sqrt {2}}}}+{\sqrt {2}}+1}{4}}a^{2}\Leftrightarrow$

$\Leftrightarrow S_{16}={\frac {1}{2}}P_{16}r,\ P_{16}=16a,\ r={\frac {{\sqrt {4+2{\sqrt {2}}}}+{\sqrt {2}}+1}{2}}a\Leftrightarrow$

$\Leftrightarrow S_{16}=4{\sqrt {2-{\sqrt {2}}}}R^{2},\ R={\sqrt {8+4{\sqrt {2}}+4{\sqrt {2+{\sqrt {2}}}}+2{\sqrt {4+2{\sqrt {2}}}}}}a\Leftrightarrow$

$\Leftrightarrow S_{16}=16\left({\sqrt {4+2{\sqrt {2}}}}-{\sqrt {2}}-1\right)r^{2},\ r={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}R,$

где

$\sin {\frac {\pi }{16}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}{2}},\ \cos {\frac {\pi }{16}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}$

$tg{\frac {\pi }{16}}={\sqrt {4+2{\sqrt {2}}}}-{\sqrt {2}}-1,\ ctg{\frac {\pi }{16}}={\sqrt {4+2{\sqrt {2}}}}+{\sqrt {2}}+1.$

Другие многоугольники:

• треугольник (тригон);
• четырёхугольник (тетрагон);
• пятиугольник (пентагон);
• шестиугольник (гексагон);
• семиугольник (гептагон);
• восьмиугольник (октагон);
• девятиугольник (эннеагон);
• десятиугольник (декагон);
• одиннадцатиугольник (гендекагон);
• двенадцатиугольник (додекагон);
• тринадцатиугольник (тридекагон);
• четырнадцатиугольник (тетрадекагон);
• пятнадцатиугольник (пентадекагон);
• шестнадцатиугольник (гексадекагон);
• семнадцатиугольник (гептадекагон);
• восемнадцатиугольник (октадекагон);
• девятнадцатиугольник (эннеадекагон);
• двадцатиугольник (икосагон);
• правильный n-угольник.