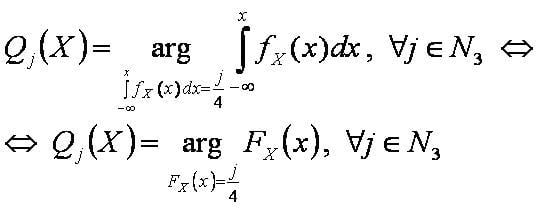Квартиль непрерывной случайной величины

Квартиль — это числовая характеристика случайной величины, характеризующая четверти совокупности.

Обозначения

X — случайная величина;

f_X(x) — дифференциальная функция распределения — функция плотности вероятности;

F_X(x) — интегральная функция распределения — функция вероятности;

Q_j(x) — квартиль, характеризующая j четвертей совокупности, — это граница между j-ой и j+1-ой частями.

Формулы

$Q_{j}(X)=\arg \limits _{\int \limits _{-\infty }^{x}f_{X}(x)dx={\frac {j}{4}}}\ \int \limits _{-\infty }^{x}f_{X}(x)dx,\ \forall j\in N_{3}\Leftrightarrow$

$\Leftrightarrow Q_{j}(X)=\arg \limits _{F_{X}(x)={\frac {j}{4}}}\ F_{X}(x),\ \forall j\in N_{3}$

• Квартиль Q₂(x) равна медиане Me(x).

См. также

• Квартиль дискретной случайной величины

Другие формулы:

• средняя;
• дисперсия;
• среднеквадратическое отклонение;
• среднее линейное отклонение;
• мода;
• медиана;
• квартиль;
• дециль;
• начальный момент k-ого порядка;
• центральный момент k-ого порядка;
• коэффициент асимметрии;
• коэффициент эксцесса.

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970, стр.487.