Математика как иерархия знаковых систем
Математика как иерархия знаковых систем — условное название совокупности взглядов на математику, согласно которым математика не является эмпирической наукой, а каждый раздел математики представляет собой лишь знаковую модель для той или иной совокупности отношений, устанавливаемых эмпирическими (опытными, содержательными науками).
Из данного подхода вытекает, что математика свободна от опыта в своем развитии, а именно — она может создавать новые понятия и концепции, не ссылаясь на опыт, реальные отношения и аналогии, взятые из наблюдаемого мира.
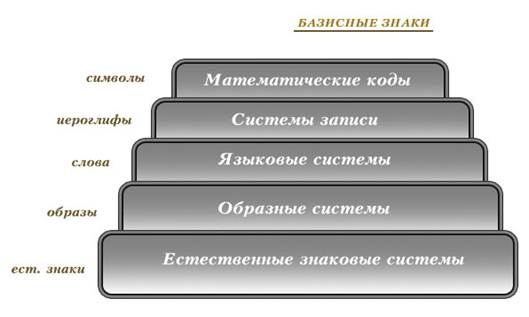
Подобный подход излагается в книге «Некоторые особенности математического знания» (авторы — Беляев Е. А., Киселева Н. А., Перминов В. Я., 1975 г.). Понятие иерархии знаковых систем также развивалось в работах Абрама Соломоника в 1990-е годы, математические знаковые системы занимают наивысшее место в построенной им иерархии.
Эволюция взглядов на эмпиризм математики[править]
Начиная с древних времен и примерно до конца XVIII столетия математика воспринималась как близкая к физике наука, изучающая некоторый круг свойств природы. Этот подход восходит к Аристотелю, отметившему в работе «Метафизика», что Геометрия (тогдашнее название математики) и Астрономия «занимаются отдельными областями сущего». Аксиомы Евклида апеллировали к чувственным образам восприятия реального мира, то есть предполагалось, что геометрия описывает общие свойства природы. В рамках подобного эмпирического подхода каждое математическое понятие, теорема или теория должны иметь реальный образ или наглядное истолкование, апеллирующее к физическому (содержательному) смыслу, который оправдывает введение математической теории и используемых ей терминов.
Исходя из этих требований математики XVII—XVIII веков придумывали обоснования появляющимся новым абстрактным понятиям, например таким, как введенные в рассмотрение отрицательные, иррациональные и комплексные числа. Появление начал анализа, рассмотрение бесконечно малых величин вызвало попытки выявления объективной сути понятия бесконечности, в частности разрешения проблемы бесконечной делимости материи для нужд обоснования математического анализа.
В настоящее время эти попытки обоснования абстрактных математических понятий аналогиями из реального мира считаются неудовлетворительными. Одним из первых, кто понял необязательность содержательного обоснования абстрактных образов, стал французский математик Лазарь Карно (1753—1823). Он считал отрицательные, комплексные числа, бесконечно большие и бесконечные малые величины фиктивными сущностями, которые употребляются вспомогательным образом как термины сравнения для сопоставления и выявления зависимостей между «истинными» количествами.[1] Практически одновременно с Карно против эмпирического обоснования математики выступал русский математик С. Е. Гурьев (1764—1813).[2]
О. Коши в начале XIX века дал строгое обоснование анализа, не привлекая понятия бесконечно малой и бесконечно большой величины, а на базе теорий Дедекинда и Кантора были обоснованы вещественные, а также комплексные числа.
В соответствии с развившимся тогда подходом, применяемым до настоящего времени, достаточно установить формальную непротиворечивость новых математических понятий и теорий, а не искать их эмпирического истолкования. Этим же подходом обосновывается законность неевклидовых геометрий — путем установления их непротиворечивости.
Развивается понимание сути математики как особого языка. Так ее характеризуют, в частности Н. Бор, Р. Фейнман. Целью математики при этом является разработка формальных систем для различных систем содержательных утверждений (см. также Математизация научного знания). Математическое описание содержательной области, как правило, позволяет получить такие следствия, которые невозможно вывести, оставаясь в рамках содержательного языка. Это показывает, что математика — совокупность знаковых моделей для содержательных представлений.
В связи с эволюцией взглядов на то, что представляет собой математика, предпринимаются многочисленные попытки дать ей определение, раскрывающее ее предмет и смысл. В. Я. Перминов говорит, что попытки дать единственное наиболее точное определение математики представляет собой предрассудок, идущий от средневековой философии, а математика может быть определена различными способами (в том числе как язык или иерархия знаковых систем.
Абстрактная математика и ее развитие[править]
В. Я. Перминов в книге «Некоторые особенности математического знания» строит следующую схему. Он обозначает М1Ф1 область непосредственного совпадения двух пересекающихся кругов, которая соответствует совокупности математических теорий, имеющих эмпирическую (физическую) интерпретацию и одновременно физических (содержательных) теорий, имеющих адекватное математическое представление. При этом существуют как математические теории (структуры), не имеющие в настоящее время физической (эмпирической) интерпретации и применения на практике, совокупность которых обозначается М2, так и физические (содержательные) теории, пока не нашедшие адекватной математической модели (их совокупность обозначается Ф2).
Перминов указывает в рамках данных обозначений, что «сама возможность построения системы образов М2 обеспечивается символическим характером математического знания». Формальные правила обращения с символами дают возможность повышать уровень абстракции, не прибегая к содержательным интерпретациям получаемых математических образов. Такая возможность характерна только для математики, которая таким образом наиболее абстрактна по сравнению с остальными науками (см. также Математизация научного знания).
Мотивы построения новых образов из области М2:
- за счет новых абстракций от образов М1 (так возникли структуры группы, упорядоченного множества, пространства и др.);
- из-за необходимости введения новых формальных определений для осуществления промежуточных операций (классическим примером может быть введение комплексных чисел для решения любых кубических уравнений по формуле Кардано, другой пример — введение Диофантом отрицательных чисел и операций с ними для решения уравнений);
- как результат трансформации некоторой теории из М1 (так из евклидовой геометрии получилась плеяда неевклидовых геометрий, начиная с геометрии Лобачевского);
- в качестве существенных для чистой математики «интересных» примеров и особенно — контрпримеров, позволяющих сконструировать новый математический объект (непрерывные функции, не имеющие производной, кривая Пеано, ковер Серпинского, группы с неразрешимой задачей тождества слов и др.);
- из-за стремления математики в силу ее красоты к логической простоте и симметрии (например правильные многогранники — «платоновы тела», простые алгебры Ли).
См. также[править]
Источники[править]
Литература[править]
- Абрам Соломоник. Философия знаковых систем и язык — Минск: «МЕТ», 2002.
- Беляев Е. А., Киселева Н. А., Перминов В. Я. Некоторые особенности математического знания — М.: Издательство Московского университета, 1975. Глава I. Математика как иерархия знаковых систем.