Площадь поверхности параллелепипеда

Параллелепипед

Площадь поверхности параллелепипеда — это сумма площадей его (параллелепипеда) граней.

Параллелепипед — это шестигранник с параллельными противоположными гранями (параллелограммами).

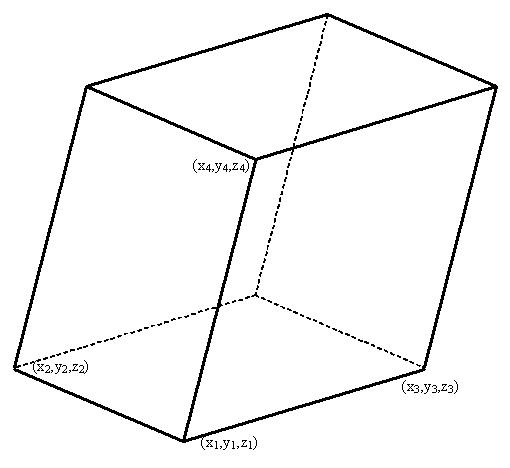
Рассмотрим параллелепипеды, в которых заданы четыре точки 1, 2, 3, 4, причём точки 2, 3, 4 являются соседними для точки 1.

Обозначения

Введём обозначения:

[math]\bar r_1=(x_1,y_1,z_1)[/math] — радиус-вектор первой точки;

[math]\bar r_2=(x_2,y_2,z_2)[/math] — радиус-вектор второй точки;

[math]\bar r_3=(x_3,y_3,z_3)[/math] — радиус-вектор третьей точки;

[math]\bar r_4=(x_4,y_4,z_4)[/math] — радиус-вектор четвёртой точки;

[math]\bar n=(A,B,C)[/math] — нормаль к плоскости, проходящей через три заданные точки;

S_Δ — площадь треугольника, построенного по трём заданным точкам;

S_пар — площадь поверхности параллелепипеда, построенного по четырём заданным точкам.

Формула

где

См. также

• Объём параллелепипеда

Другие многогранники

• призма;
• пирамида;
• усечённая пирамида;
• тетраэдр;
• параллелепипед;
• n-гранник.

Ссылки

• Участник:Logic-samara