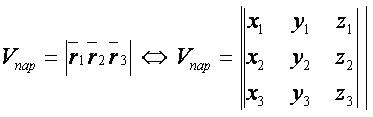Объём параллелепипеда

Параллелепипед

Объём параллелепипеда — это число, характеризующее параллелепипед в единицах измерения объёма.

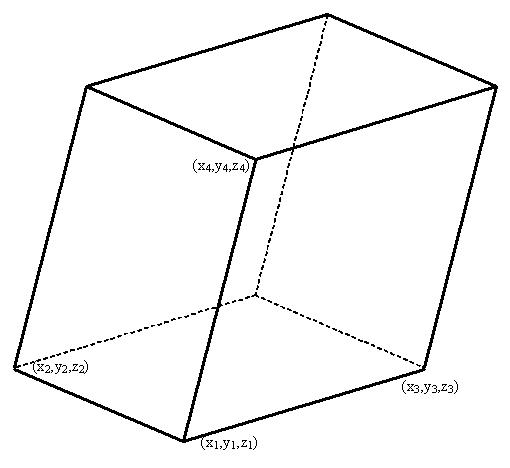
Параллелепипед — это шестигранник с параллельными противоположными гранями (параллелограммами).

Обозначения

Введём обозначения:

[math]\displaystyle{ \bar r_1=(x_1,y_1,z_1) }[/math] — радиус-вектор первой точки;

[math]\displaystyle{ \bar r_2=(x_2,y_2,z_2) }[/math] — радиус-вектор второй точки;

[math]\displaystyle{ \bar r_3=(x_3,y_3,z_3) }[/math] — радиус-вектор третьей точки;

[math]\displaystyle{ \bar r_4=(x_4,y_4,z_4) }[/math] — радиус-вектор четвёртой точки;

V_пар — объём параллелепипеда, построенного по четырём заданным точкам.

Формула

Если четвёртую точку взять в начале координат, то формула упрощается до следующей:

См. также

• Площадь поверхности параллелепипеда

Другие многогранники

• Объём призмы;
• Объём пирамиды;
• Объём усечённой пирамиды;
• Объём тетраэдра;
• Объём параллелепипеда;
• Объём n-гранника.

Другие формулы

• объём многогранника;
• объём правильного многогранника;
• объём трёхмерной фигуры;
• объём фигуры вращения.

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970. стр.76.

Ссылки

• Участник:Logic-samara