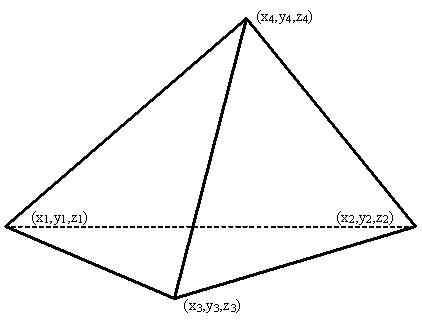
Площадь поверхности тетраэдра

Тетраэдр

Площадь поверхности тетраэдра — это сумма площадей его (тетраэдра) граней.

Тетраэдр — это четырёхгранник с гранями из треугольников.

Обозначения

Введём обозначения:

${\bar {r}}_{1}=(x_{1},y_{1},z_{1})$ — радиус-вектор первой точки;

${\bar {r}}_{2}=(x_{2},y_{2},z_{2})$ — радиус-вектор второй точки;

${\bar {r}}_{3}=(x_{3},y_{3},z_{3})$ — радиус-вектор третьей точки;

${\bar {r}}_{4}=(x_{4},y_{4},z_{4})$ — радиус-вектор четвёртой точки;

${\bar {n}}=(A,B,C)$ — нормаль к плоскости, проходящей через три заданные точки;

S_Δ — площадь грани тетраэдра, построенной по трём заданным точкам;

S_тетр — площадь поверхности тетраэдра, построенного по четырём заданным точкам.

Формулы

$S_{\text{тетр}}={\frac {1}{2}}\left(\left|{\bar {n}}_{123}\right|+\left|{\bar {n}}_{124}\right|+\left|{\bar {n}}_{134}\right|+\left|{\bar {n}}_{234}\right|\right)\Leftrightarrow S_{\text{тетр}}=S_{\triangle 123}+S_{\triangle 124}+S_{\triangle 134}+S_{\triangle 234}$

где

$S_{\triangle 123}={\frac {1}{2}}{\sqrt {{\begin{vmatrix}1&y_{1}&z_{1}\\1&y_{2}&z_{2}\\1&y_{3}&z_{3}\end{vmatrix}}^{2}+{\begin{vmatrix}x_{1}&1&z_{1}\\x_{2}&1&z_{2}\\x_{3}&1&z_{3}\end{vmatrix}}^{2}+{\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{vmatrix}}^{2}}}$

$S_{\triangle 124}={\frac {1}{2}}{\sqrt {{\begin{vmatrix}1&y_{1}&z_{1}\\1&y_{2}&z_{2}\\1&y_{4}&z_{4}\end{vmatrix}}^{2}+{\begin{vmatrix}x_{1}&1&z_{1}\\x_{2}&1&z_{2}\\x_{4}&1&z_{4}\end{vmatrix}}^{2}+{\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{4}&y_{4}&1\end{vmatrix}}^{2}}}$

$S_{\triangle 134}={\frac {1}{2}}{\sqrt {{\begin{vmatrix}1&y_{1}&z_{1}\\1&y_{3}&z_{3}\\1&y_{4}&z_{4}\end{vmatrix}}^{2}+{\begin{vmatrix}x_{1}&1&z_{1}\\x_{3}&1&z_{3}\\x_{4}&1&z_{4}\end{vmatrix}}^{2}+{\begin{vmatrix}x_{1}&y_{1}&1\\x_{3}&y_{3}&1\\x_{4}&y_{4}&1\end{vmatrix}}^{2}}}$

$S_{\triangle 234}={\frac {1}{2}}{\sqrt {{\begin{vmatrix}1&y_{2}&z_{2}\\1&y_{3}&z_{3}\\1&y_{4}&z_{4}\end{vmatrix}}^{2}+{\begin{vmatrix}x_{2}&1&z_{2}\\x_{3}&1&z_{3}\\x_{4}&1&z_{4}\end{vmatrix}}^{2}+{\begin{vmatrix}x_{2}&y_{2}&1\\x_{3}&y_{3}&1\\x_{4}&y_{4}&1\end{vmatrix}}^{2}}}$

См. также

• Объём тетраэдра
• Tetra Classic

Другие многогранники

• призма;
• пирамида;
• усечённая пирамида;
• тетраэдр;
• параллелепипед;
• n-гранник.

Другие формулы

Площадь:

• многоугольника;
• правильного многоугольника;
• n-угольника Рёло;
• плоской фигуры;
• площадь поверхности:
  • многогранника;
  • правильного многогранника;
  • фигуры вращения.