Площадь прямоугольного треугольника

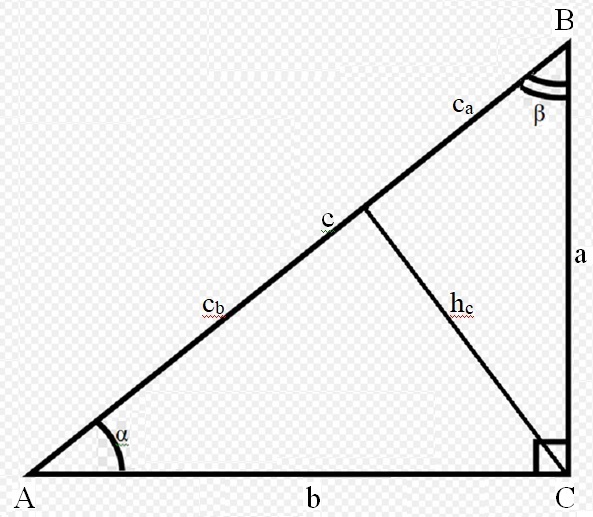
Прямоугольный треугольник

Площадь прямоугольного треугольника — число, характеризующее прямоугольный треугольник в единицах измерения площади.

Определение

Прямоугольный треугольник — треугольник у которого один угол прямой, лежащий напротив стороны называемой гипотенузой, стороны прилежащие к прямому углу называются катетами.

Обозначения

a — первый катет — первая сторона;

b — второй катет — вторая сторона;

c — гипотенуза — третья сторона;

h_c — высота, опущенная на сторону c;

p — полупериметр треугольника;

r — радиус вписанной окружности;

R — радиус описанной окружности;

S_прямΔ — площадь прямоугольного треугольника.

Формулы:

$S_{{\text{прям}}\triangle }={\frac {1}{2}}ab\Leftrightarrow S_{{\text{прям}}\triangle }={\frac {1}{2}}ch_{c},\ h_{c}={\frac {ab}{c}},\ c={\sqrt {a^{2}+b^{2}}}\Leftrightarrow$

$\Leftrightarrow S_{{\text{прям}}\triangle }={\frac {(a+b+c)(a+b-c)}{4}}\Leftrightarrow S_{{\text{прям}}\triangle }=pr,\ p={\frac {a+b+c}{2}},\ r={\frac {a+b-c}{2}}\Leftrightarrow$

$\Leftrightarrow S_{{\text{прям}}\triangle }=r^{2}+rc,\ r={\frac {a+b-{\sqrt {a^{2}+b^{2}}}}{2}},\ c={\sqrt {a^{2}+b^{2}}}\Leftrightarrow$

$\Leftrightarrow S_{{\text{прям}}\triangle }={\frac {abR}{c}},\ R={\frac {c}{2}},\ c={\sqrt {a^{2}+b^{2}}}\Leftrightarrow$

$\Leftrightarrow S_{{\text{прям}}\triangle }=Rh_{c},\ R={\frac {\sqrt {a^{2}+b^{2}}}{2}},\ h_{c}={\frac {ab}{\sqrt {a^{2}+b^{2}}}}$

Другие многоугольники

• треугольник:
  • равносторонний треугольник;
  • прямоугольный треугольник;
  • равнобедренный треугольник;
• четырёхугольник:
  • квадрат;
  • прямоугольник;
  • ромб;
  • параллелограмм;
  • трапеция;
• n-угольник.

См.также

• Площадь треугольника
• Площадь равнобедренного треугольника