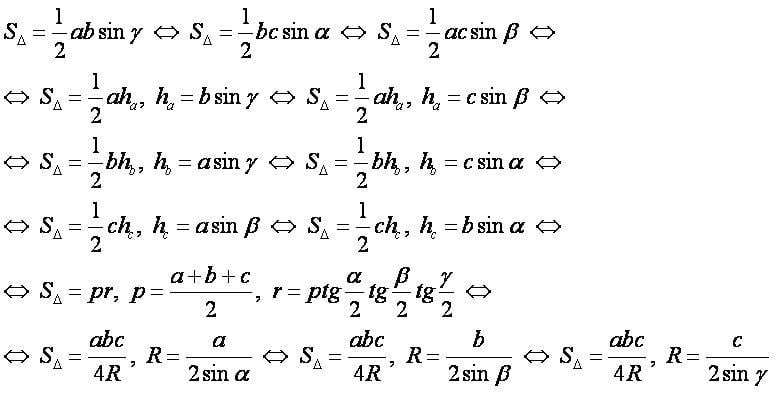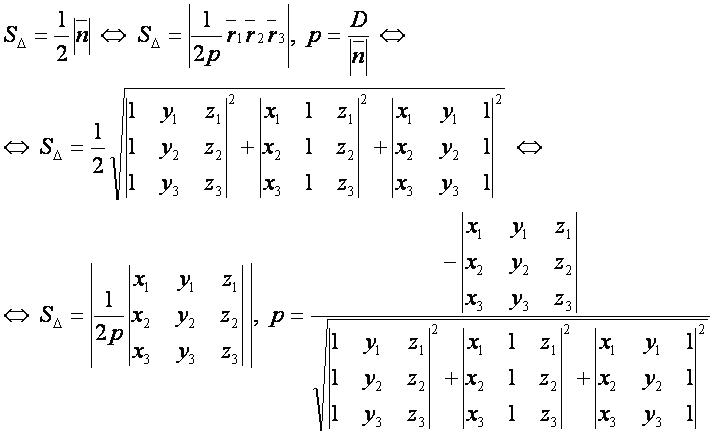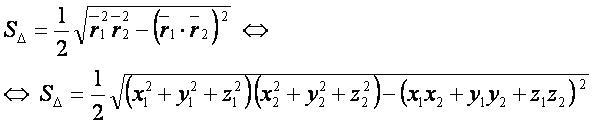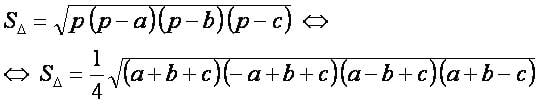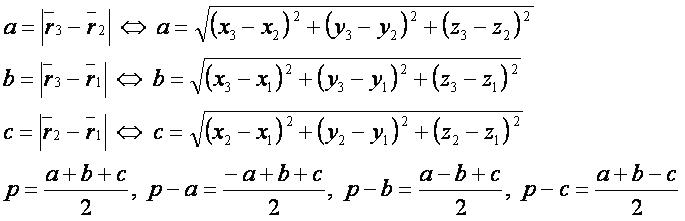Площадь треугольника

Треугольник

Математика. Урок 8. Площадь треугольника // novykrug [5:54]

Площадь треугольника — положительное действительное число, характеризующее треугольник в единицах измерения площади.

Обозначения

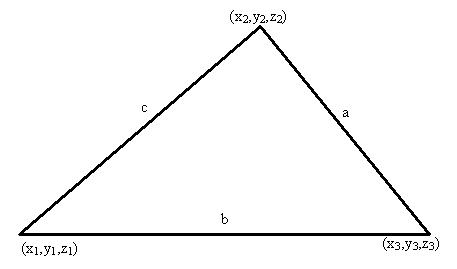
a — первая сторона;

b — вторая сторона;

c — третья сторона;

h_a — высота, опущенная на сторону a;

h_b — высота, опущенная на сторону b;

h_c — высота, опущенная на сторону c;

α — угол напротив стороны a;

β — угол напротив стороны b;

γ — угол напротив стороны c;

p — полупериметр треугольника;

r — радиус вписанной окружности;

R — радиус описанной окружности;

S_Δ — площадь треугольника.

Формулы

Формулы в векторной и координатной форме

${\bar {r}}_{1}=(x_{1},y_{1},z_{1})$ — радиус-вектор первой точки;

${\bar {r}}_{2}=(x_{2},y_{2},z_{2})$ — радиус-вектор второй точки;

${\bar {r}}_{3}=(x_{3},y_{3},z_{3})$ — радиус-вектор третьей точки;

${\bar {n}}=(A,B,C)$ — нормаль к плоскости, проходящей через заданные точки;

p — отклонение начала координат от плоскости, проходящей через заданные точки;

S_Δ — площадь треугольника, построенного по трём заданным точкам.

• Формула с параметром p применима, только когда p≠0.

Если третью точку взять в начале координат, то можно применять следующую формулу:

Формула Герона

a — длина стороны треугольника, расположенной между второй и третьей точками;

b — длина стороны треугольника, расположенной между первой и третьей точками;

c — длина стороны треугольника, расположенной между первой и второй точками;

p — полупериметр треугольника, построенного по трём заданным точкам.

где

Другие многоугольники:

• треугольник:
  • равносторонний треугольник;
  • прямоугольный треугольник;
  • равнобедренный треугольник;
• четырёхугольник:
  • квадрат;
  • прямоугольник;
  • ромб;
  • параллелограмм;
  • трапеция;
• n-угольник.

См. также

• Площадь равностороннего треугольника
• Площадь равнобедренного треугольника
• Площадь прямоугольного треугольника
• Площадь треугольника Рёло

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970. стр.75.
• Бронштейн М. Н., Семендяев К. А., Справочник по математике — М., 1956, стр.166, стр.187.

Ссылки

• Участник:Logic-samara