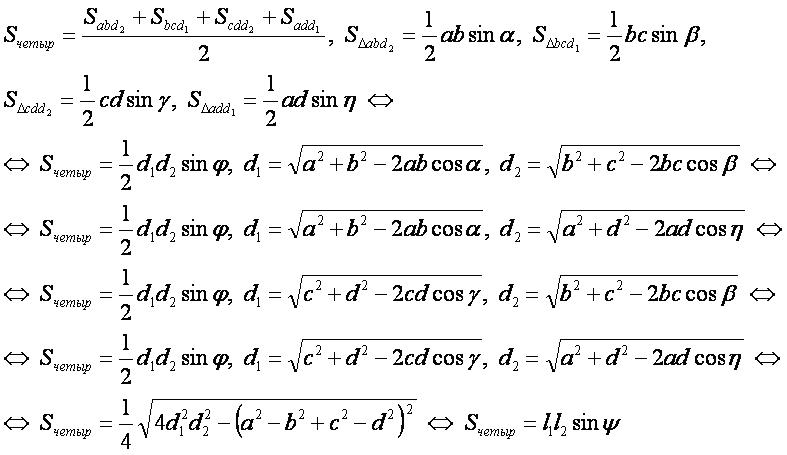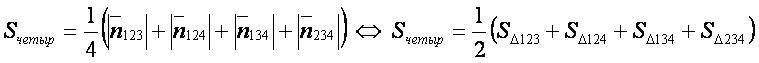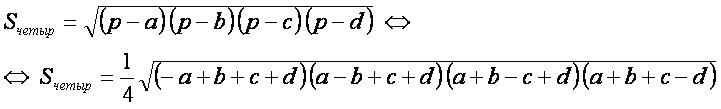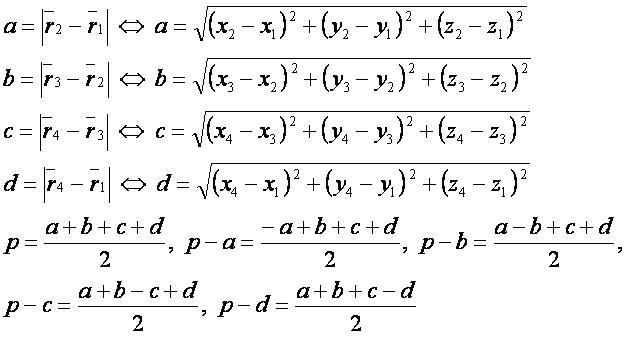Площадь четырёхугольника

Площади четырехугольников. Геометрия 7-9 классы. Урок 34 // MathTutor [19:24]

Площадь четырёхугольника — действительное число, характеризующее четырёхугольник в единицах измерения площади.

Для выпуклых четырёхугольников все четыре точки углов лежат в одной плоскости и для любых его (четырёхугольника) двух точек все точки отрезка принадлежат четырёхугольнику.

Обозначения

a — первая сторона;

b — вторая сторона;

c — третья сторона;

d — четвёртая сторона;

α — угол между сторонами a и b;

β — угол между сторонами b и c;

γ — угол между сторонами c и d;

η — угол между сторонами a и d;

d₁ — диагональ, соединяющая вершины углов α и γ;

d₂ — диагональ, соединяющая вершины углов β и η;

l₁ — средняя линия, соединяющая середины сторон a и c;

l₂ — средняя линия, соединяющая середины сторон b и d;

φ — угол (острый) между диагоналями;

ψ — угол (острый) между средними линиями;

p — полупериметр четырёхугольника;

S_Δ — площадь треугольника;

S_четыр — площадь четырёхугольника.

Формулы

Формулы в векторной и координатной форме

Обозначения:

${\bar {r}}_{1}=(x_{1},y_{1},z_{1})$ — радиус-вектор первой точки;

${\bar {r}}_{2}=(x_{2},y_{2},z_{2})$ — радиус-вектор второй точки;

${\bar {r}}_{3}=(x_{3},y_{3},z_{3})$ — радиус-вектор третьей точки;

${\bar {r}}_{4}=(x_{4},y_{4},z_{4})$ — радиус-вектор четвёртой точки;

${\bar {n}}=(A,B,C)$ — нормаль к плоскости, проходящей через три заданные точки;

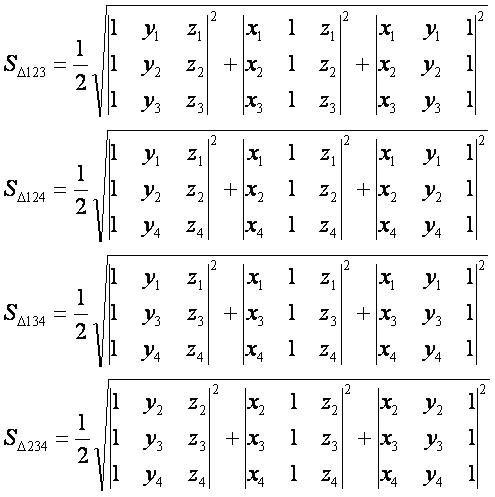
S_Δ — площадь треугольника, построенного по трём заданным точкам;

S_четыр — площадь четырёхугольника, построенного по четырём заданным точкам.

где

Формула Брахмагупты

Для четырёхугольника, вокруг которых можно описать окружность и у которого порядок следования вершин 1, 2, 3, 4, для нахождения их площади можно использовать формулу Брахмагупты.

Обозначения:

a — длина стороны четырёхугольника, расположенной между первой и второй точками;

b — длина стороны четырёхугольника, расположенной между второй и третьей точками;

c — длина стороны четырёхугольника, расположенной между третьей и четвёртой точками;

d — длина стороны четырёхугольника, расположенной между первой и четвёртой точками;

p — полупериметр четырёхугольника, построенного по четырём заданным точкам.

где

• Когда одна из сторон четырёхугольника стремится к нулю, тогда формула Брахмагупты превращается в формулу Герона для площади треугольника.
• Когда четырёхугольник является прямоугольником и a≠b, тогда формула Брахмагупты превращается в формулу площади прямоугольника, S_{прямоуг}=ab, где c=a, d=b, p=a+b.
• Когда четырёхугольник является равнобедренной трапецией и b=d, тогда формула Брахмагупты превращается в формулу площади трапеции, S_{равн.трап}=h(a+c)/2, где h²=(p-a)(p-c), p-b=(a+c)/2.

Один из методов определения площади четырехугольника состоит в разбиении фигуры на два треугольника с помощью диагонали и в вычислении суммы площадей образовавшихся треугольников.

См.также

• Площадь трапеции
• Площадь параллелограмма
• Площадь прямоугольника
• Площадь ромба
• Площадь квадрата

Литература

• Бронштейн М. Н., Семендяев К. А., Справочник по математике — М., 1956, стр.167.

Другие многоугольники

• треугольник:
  • равносторонний треугольник;
  • прямоугольный треугольник;
  • равнобедренный треугольник;
• четырёхугольник:
  • квадрат;
  • прямоугольник;
  • ромб;
  • параллелограмм;
  • трапеция;
• n-угольник.