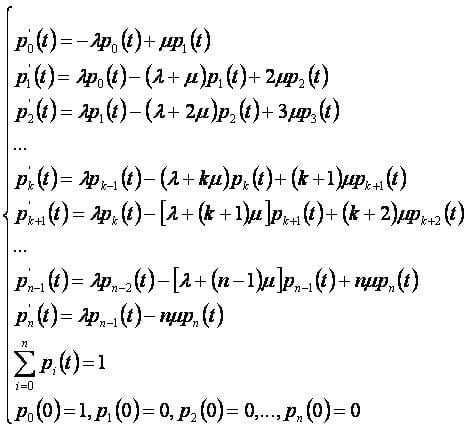СМО с отказами

Многоканальные системы с отказами [8:04]

Математическая модель СМО с отказами

СМО с отказами — это система массового обслуживания, в которой есть каналы обслуживания, но нет очереди: если заявка приходит, в момент, когда все каналы свободны, то она немедленно обслуживается любым одним каналом, если заявка приходит — когда уже обслуживаются заявки числом меньше, чем число каналов, то она немедленно обслуживается одним из свободных каналов, иначе если заявка приходит — когда заняты все каналы, то заявка покидает систему (теряется).

Описание модели

На вход n-канальной СМО поступает простейший поток заявок с интенсивностью λ.

Интенсивность простейшего потока обслуживания каждого канала μ.

Если заявка застаёт все каналы свободными, она принимается на обслуживание и обслуживается любым одним из n-каналов.

Если заявка застаёт свободным хотя бы один канал, то она принимается на обслуживание любым из свободных каналов и обслуживается до конца.

Если заявка застаёт все каналы занятыми, то она получает отказ (покидает систему не обслуженной).

После окончания обслуживания одной заявки освобождается один канал.

Состояние рассмотренной системы будем связывать с числом заявок, находящихся в системе.

Граф состояний

Рассмотрим множество состояний системы:

S₀ — в системе нет ни одной заявки, все каналы свободны;

S₁ — в системе имеется одна заявка, она обслуживается одним каналом;

S₂ — в системе имеется две заявки, они обслуживается двумя каналами;

…;

S_k — в системе имеется k-заявок, они обслуживаются k-каналами;

S_k+1 — в системе имеется (k+1)-заявок, они обслуживаются (k+1)-каналами;

…;

S_n-1 — в системе имеется (n-1)-заявок, они обслуживаются (n-1)-каналами;

S_n — в системе имеется n-заявок, они обслуживаются n-каналами.

Система дифференциальных уравнений

Система дифференциальных уравнений, описывающих поведение системы, имеет вид:

${\begin{cases}p_{0}'(t)=-\lambda p_{0}(t)+\mu p_{1}(t)\\p_{1}'(t)=\lambda p_{0}(t)-(\lambda +\mu )p_{1}(t)+2\mu p_{2}(t)\\p_{2}'(t)=\lambda p_{1}(t)-(\lambda +2\mu )p_{2}(t)+3\mu p_{3}(t)\\\ldots \\p_{k}'(t)=\lambda p_{k-1}(t)-(\lambda +k\mu )p_{k}(t)+(k+1)\mu p_{k+1}(t)\\p_{k+1}'(t)=\lambda p_{k}(t)-(\lambda +(k+1)\mu )p_{k+1}(t)+(k+2)\mu p_{k+2}(t)\\\ldots \\p_{n-1}'(t)=\lambda p_{n-2}(t)-(\lambda +(n-1)\mu )p_{n-1}(t)+n\mu p_{n}(t)\\p_{n}'(t)=\lambda p_{n-1}(t)-n\mu p_{n}(t)\\\sum \limits _{i=0}^{n}p_{i}(t)=1\\p_{0}(0)=1,\ p_{1}(0)=0,\ p_{2}(0)=0,\ldots ,\ p_{n}(0)=0\end{cases}}$

Рассмотрим стационарный режим работы системы (при t → ∞).

Система уравнений принимает вид:

${\begin{cases}-\lambda p_{0}+\mu p_{1}=0\\\lambda p_{0}-(\lambda +\mu )p_{1}+2\mu p_{2}=0\\\lambda p_{1}-(\lambda +2\mu )p_{2}+3\mu p_{3}=0\\\ldots \\\lambda p_{k-1}-(\lambda +k\mu )p_{k}+(k+1)\mu p_{k}=0\\\lambda p_{k}-(\lambda +(k+1)\mu )p_{k+1}+(k+2)\mu p_{k+1}=0\\\ldots \\\lambda p_{n-2}-(\lambda +(n-1)\mu )p_{n-1}+n\mu p_{n}=0\\\lambda p_{n-1}-n\mu p_{n}=0\\\sum \limits _{i=0}^{n}p_{i}=1\end{cases}}$ $\Leftrightarrow$ ${\begin{cases}-\lambda p_{0}+\mu p_{1}=0\\-\lambda p_{1}+2\mu p_{2}=0\\-\lambda p_{2}+3\mu p_{3}=0\\\ldots \\-\lambda p_{k}+(k+1)\mu p_{k+1}=0\\-\lambda p_{k+1}+(k+2)\mu p_{k+2}=0\\\ldots \\-\lambda p_{n-1}+n\mu p_{n}=0\\\lambda p_{n-1}-n\mu p_{n}=0\\\sum \limits _{i=0}^{n}p_{i}=1\end{cases}}$

Суммируя в системе уравнения с первого до i-го (i=1, …, n), получаем упрощённый вид системы.

Решим систему относительно p₀,p₁, …, p_n.

${\begin{cases}p_{1}={\frac {\lambda }{\mu }}p_{0}\\p_{2}={\frac {\lambda }{2\mu }}p_{1}\\p_{3}={\frac {\lambda }{3\mu }}p_{2}\\\ldots \\p_{k+1}={\frac {\lambda }{(k+1)\mu }}p_{k}\\p_{k+2}={\frac {\lambda }{(k+2)\mu }}p_{k+1}\\\ldots \\p_{n-1}={\frac {\lambda }{(n-1)\mu }}p_{n-2}\\p_{n}={\frac {\lambda }{n\mu }}p_{n-1}\\\sum \limits _{i=0}^{n}p_{i}=1\end{cases}}$ $\Leftrightarrow$ ${\begin{cases}p_{1}={\frac {\lambda }{\mu }}p_{0}\\p_{2}={\frac {1}{2!}}\left({\frac {\lambda }{\mu }}\right)^{2}p_{0}\\p_{3}={\frac {1}{3!}}\left({\frac {\lambda }{\mu }}\right)^{3}p_{0}\\\ldots \\p_{k+1}={\frac {1}{(k+1)!}}\left({\frac {\lambda }{\mu }}\right)^{k+1}p_{0}\\p_{k+2}={\frac {1}{(k+2)!}}\left({\frac {\lambda }{\mu }}\right)^{k+2}p_{0}\\\ldots \\p_{n-1}={\frac {1}{(n-1)!}}\left({\frac {\lambda }{\mu }}\right)^{n-1}p_{0}\\p_{n}={\frac {1}{n!}}\left({\frac {\lambda }{\mu }}\right)^{n}p_{0}\\\sum \limits _{i=0}^{n}{\frac {1}{i!}}\left({\frac {\lambda }{\mu }}\right)^{i}p_{0}=1\end{cases}}$ $\Leftrightarrow$ ${\begin{cases}p_{0}=\left(\sum \limits _{i=0}^{n}{\frac {\lambda ^{i}}{i!\mu ^{i}}}\right)^{-1}\\p_{1}={\frac {\lambda }{\mu }}p_{0}\\\ldots \\p_{i}={\frac {\lambda ^{i}}{i!\mu ^{i}}}p_{0}\\\ldots \\p_{n}={\frac {\lambda ^{n}}{n!\mu ^{n}}}p_{0}\end{cases}}$

В результате получаем решение системы: $p_{0}={\frac {1}{\sum \limits _{i=0}^{n}{\frac {\lambda ^{i}}{i!\mu ^{i}}}}},\ p_{i}={\frac {\lambda ^{i}}{i!\mu ^{i}}}p_{0},\forall i\in N_{n}$

Основные характеристики системы

$t_{\lambda }={\frac {1}{\lambda }},t_{\mu }={\frac {1}{\mu }},\rho ={\frac {\lambda }{\mu }},\chi ={\frac {\lambda }{n\mu }},$

$p_{0}={\frac {1}{\sum \limits _{i=0}^{n}{\frac {\rho ^{i}}{i!}}}}={\frac {1}{1+{\frac {\rho }{1!}}+{\frac {\rho ^{2}}{2!}}+\ldots +{\frac {\rho ^{n}}{n!}}}},p_{i}={\frac {\rho ^{i}}{i!}}p_{0},\forall i\in N_{n},$

${\bar {s}}={\sum \limits _{i=0}^{n}{ip_{i}}}=\rho (1-p_{n})=\rho \left(1-{\frac {\rho ^{n}}{n!}}p_{0}\right),{\bar {r}}=0,{\bar {l}}={\bar {s}},{\bar {k}}={\bar {s}},$

$q=1-p_{n}=1-{\frac {\rho ^{n}}{n!}}p_{0},A=\lambda (1-p_{n})=\lambda \left(1-{\frac {\rho ^{n}}{n!}}p_{0}\right),$

$p_{\text{прост.}}=p_{0},p_{\text{отк.}}=p_{n}={\frac {\rho ^{n}}{n!}}p_{0},p_{\text{обсл.}}=1-p_{n}=1-{\frac {\rho ^{n}}{n!}}p_{0},$

$p_{\text{п.загр.}}=p_{n}={\frac {\rho ^{n}}{n!}}p_{0},p_{\text{н.загр.}}=\sum \limits _{i=0}^{n-1}p_{i}=\sum \limits _{i=0}^{n-1}{\frac {\rho ^{i}}{i!}}p_{0}=1-p_{n}=1-{\frac {\rho ^{n}}{n!}}p_{0},$

$p_{\text{н.очер.}}=0,p_{\text{1зан.}}={\frac {\bar {k}}{n}}={\frac {\rho }{n}}(1-p_{n})=\chi (1-p_{n}),p_{\text{1прост.}}=1-{\frac {\bar {k}}{n}}=1-\chi (1-p_{n}),$

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{п.загр.}=\frac{1}{n\mu}, \bar t_\text{н.загр.}= \bar t_\text{п.загр.}\cdot\frac{p_\text{н.загр.}}{p_\text{п.загр.}}=\frac{\sum\limits_{i=0}^{n-1}\frac{\rho^i}{i!}}{n\mu\frac{\rho^n}{n!}}=\frac{1-\frac{\rho^n}{n!}p_0}{n\mu\frac{\rho^n}{n!}p_0}=\frac{1-p_n}{ n\mu p_n}, \bar t_\text{н.очер.}=0,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{1зан.}= \bar t_\mu=\frac{1}{\mu}, \bar t_\text{1прост.}= \bar t_\text{1зан.}\cdot\frac{p_\text{1прост.}}{p_\text{1зан.}}= \frac{n-\bar k}{\mu\bar k}=\frac{1-\chi(1-p_n)}{ \mu\chi(1-p_n)},}

${\bar {t}}_{\text{прост.}}={\bar {t}}_{\lambda }={\frac {1}{\lambda }},{\bar {t}}_{\text{обсл.}}={\bar {t}}_{\lambda }\cdot {\bar {s}}={\frac {\bar {s}}{\lambda }},{\bar {t}}_{\text{очер.}}=0,{\bar {t}}_{\text{сист.}}={\bar {t}}_{\lambda }\cdot {\bar {l}}={\frac {\bar {l}}{\lambda }}.$

• Заметим, что при n=1 СМО с отказами становится одноканальной.

Другие СМО

• СМО с очередью;
• СМО с ограниченным временем ожидания;
• СМО замкнутая с очередью;
• СМО с взаимопомощью с очередью;
• СМО с отказами и взаимопомощью;
• СМО с бесконечным числом каналов;
• СМО с бесконечной очередью;
• СМО замкнутая без очереди.

Литература

• Овчаров Л. А. Прикладные задачи теории массового обслуживания — М: «Машиностроение», 1969.