СМО с очередью

Многоканальные системы с ожиданием [11:02]

Математическая модель СМО с очередью

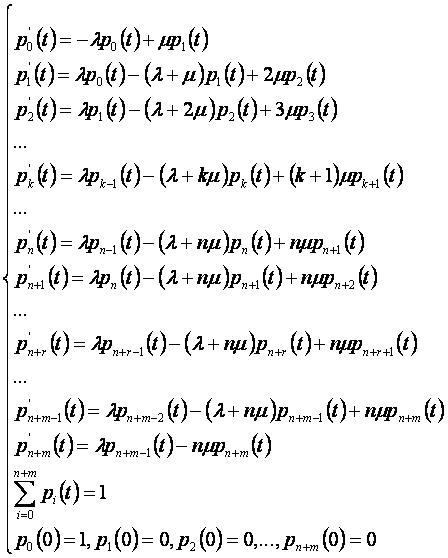
СМО с очередью — это система массового обслуживания, в которой есть места в очереди и если заявка приходит, в момент, когда все каналы заняты, то она не получает немедленно отказа, а может стать в очередь и ожидать освобождения канала, который её может обслужить.

Описание модели

На вход n-канальной СМО с m-очередью поступает простейший поток заявок с интенсивностью λ.

Интенсивность простейшего потока обслуживания каждого канала μ.

Если заявка застаёт все каналы свободными, то она принимается на обслуживание и обслуживается одним из n каналов.

После окончания обслуживания один канал освобождается.

Если вновь прибывшая заявка застаёт в системе свободным хотя бы один канал, то она принимается на обслуживание одним из свободных каналов и обслуживается до конца.

Если заявка застаёт все каналы занятыми, то она становится в очередь и «терпеливо» ждёт своего обслуживания.

Дисциплина очереди естественная: кто раньше пришёл, тот раньше и обслуживается. Максимальное число мест в очереди m.

Если вновь прибывшая заявка застаёт в очереди m-заявок, то она получает отказ и исключается из обслуживания.

Состояние рассмотренной системы будем связывать с числом заявок, находящихся в системе.

Граф состояний

Рассмотрим множество состояний системы:

S₀ — в системе нет ни одной заявки, все каналы свободны;

S₁ — в системе имеется одна заявка, она обслуживается одним каналом;

S₂ — в системе имеется две заявки, они обслуживаются двумя каналами;

…;

S_k — в системе имеется k-заявок, они обслуживаются k-каналами;

…;

S_n — в системе имеется n-заявок, они обслуживаются n-каналами, очереди нет;

S_n+1 — в системе имеется (n+1)-заявок, n из них обслуживаются n-каналами, а одна заявка ожидает в очереди;

…;

S_n+r — в системе имеется (n+r)-заявок, n из них обслуживаются n-каналами, а r-заявок ожидают в очереди;

…;

S_n+m — в системе имеется (n+m)-заявок, n из них обслуживаются n-каналами, а m-заявок ожидают в очереди;

Система дифференциальных уравнений, описывающих поведение системы, имеет вид:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{cases} p_0'(t)=-\lambda p_0(t)+\mu p_1(t) \\ p_1'(t)=\lambda p_0(t)-(\lambda +\mu)p_1(t)+2\mu p_2(t) \\ p_2'(t)=\lambda p_1(t)-(\lambda +2\mu)p_2(t)+3\mu p_3(t) \\ \ldots \\ p_k'(t)=\lambda p_{k-1}(t)-(\lambda +k\mu)p_k(t)+(k+1)\mu p_{k}(t) \\ p_{k+1}'(t)=\lambda p_{k}(t)-(\lambda +(k+1)\mu)p_{k+1}(t)+(k+2)\mu p_{k+2}(t) \\ \ldots \\ p_{n-1}'(t)=\lambda p_{n-2}(t)-(\lambda +(n-1)\mu)p_{n-1}(t)+n\mu p_{n}(t) \\ p_{n}'(t)=\lambda p_{n-1}(t)-(\lambda + n\mu)p_{n}(t)+n\mu p_{n+1}(t) \\ p_{n+1}'(t)=\lambda p_{n}(t)-(\lambda + n\mu)p_{n+1}(t)+n\mu p_{n+2}(t) \\ \ldots \\ p_{n+r}'(t)=\lambda p_{n+r-1}(t)-(\lambda + n\mu)p_{n+r}(t)+n\mu p_{n+r+1}(t) \\ \ldots \\ p_{n+m-1}'(t)=\lambda p_{n+m-2}(t)-(\lambda +n\mu)p_{n+m-1}(t)+n\mu p_{n+m}(t) \\ p_{n+m}'(t)=\lambda p_{n+m-1}(t)-n\mu p_{n+m}(t) \\ \sum\limits_{i=0}^{n+m}p_i(t)=1 \\ p_0(0)=1, \ p_1(0)=0, \ p_2(0)=0,\ldots, \ p_{n+m}(0)=0 \end{cases}}

Рассмотрим стационарный режим работы системы (при t → ∞).

Система уравнений принимает вид:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{cases} -\lambda p_0+\mu p_1=0 \\ \lambda p_0-(\lambda +\mu)p_1+2\mu p_2=0 \\ \lambda p_1-(\lambda +2\mu)p_2+3\mu p_3=0 \\ \ldots \\ \lambda p_{k-1}-(\lambda +k\mu)p_k+(k+1)\mu p_{k+1}=0 \\ \lambda p_k-(\lambda +(k+1)\mu)p_{k+1}+(k+2)\mu p_{k+2}=0 \\ \ldots \\ \lambda p_{n-2}-(\lambda +(n-1)\mu)p_{n-1}+n\mu p_n=0 \\ \lambda p_{n-1}-(\lambda +n\mu)p_n+n\mu p_{n+1}=0 \\ \lambda p_n-(\lambda +n\mu)p_{n+1}+n\mu p_{n+2}=0 \\ \ldots \\ \lambda p_{n+m-2}-(\lambda +n\mu)p_{n+m-1}+n\mu p_{n+m}=0 \\ \lambda p_{n+m-1}-n\mu p_{n+m}=0 \\ \sum\limits_{i=0}^{n+m}p_i=1 \end{cases}} Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Leftrightarrow} Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{cases} -\lambda p_0+\mu p_1=0 \\ -\lambda p_1+2\mu p_2=0 \\ -\lambda p_2+3\mu p_3=0 \\ \ldots \\ -\lambda p_k+(k+1)\mu p_{k+1}=0 \\ -\lambda p_{k+1}+(k+2)\mu p_{k+2}=0 \\ \ldots \\ -\lambda p_{n-1}+n\mu p_n=0 \\ -\lambda p_n+n\mu p_{n+1}=0 \\ -\lambda p_{n+1}+n\mu p_{n+2}=0 \\ \ldots \\ -\lambda p_{n+m-1}+n\mu p_{n+m}=0 \\ \lambda p_{n+m-1}-n\mu p_{n+m}=0 \\ \sum\limits_{i=0}^{n+m} p_i=1 \end{cases}}

Суммируя в системе уравнения с первого до i-го (i=1,n+m), получаем упрощённый вид системы.

Решим систему относительно p₀,p₁,…,p_n+m.

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{cases} p_1=\frac{\lambda}{\mu}p_0 \\ p_2=\frac{\lambda}{2\mu}p_1 \\ p_3=\frac{\lambda}{3\mu}p_2 \\ \ldots \\ p_{k+1}=\frac{\lambda}{(k+1)\mu}p_k \\ p_{k+2}=\frac{\lambda}{(k+2)\mu}p_{k+1} \\ \ldots \\ p_n=\frac{\lambda}{n)\mu}p_{n-1} \\ p_{n+1}=\frac{\lambda}{n\mu}p_n \\ p_{n+2}=\frac{\lambda}{n\mu}p_{n+1} \\ \ldots \\ p_{n+m-1}=\frac{\lambda}{n\mu}p_{n+m-2} \\ p_{n+m}=\frac{\lambda}{n\mu}p_{n+m-1} \\ \sum\limits_{i=0}^{n+m}p_i=1 \end{cases}} Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Leftrightarrow} Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{cases}p_1=\frac{\lambda}{\mu}p_0 \\ p_2=\frac{1}{2!}\left(\frac{\lambda}{\mu}\right)^2p_0 \\ p_3=\frac{1}{3!}\left(\frac{\lambda}{\mu}\right)^3p_0 \\ \ldots \\ p_{k+1}=\frac{1}{(k+1)!}\left(\frac{\lambda}{\mu}\right)^{k+1}p_0 \\ p_{k+2}=\frac{1}{(k+2)!}\left(\frac{\lambda}{\mu}\right)^{k+2}p_0 \\ \ldots \\ p_n=\frac{1}{n!}\left(\frac{\lambda}{\mu}\right)^np_0 \\ p_{n+1}=\frac{1}{n!n}\left(\frac{\lambda}{\mu}\right)^{n+1}p_0 \\ p_{n+2}=\frac{1}{n!n^2}\left(\frac{\lambda}{\mu}\right)^{n+2}p_0 \\ \ldots \\ p_{n+m-1}=\frac{1}{n!n^{m-1}}\left(\frac{\lambda}{\mu}\right)^{n+m-1}p_0 \\ p_{n+m}=\frac{1}{n!n^m}\left(\frac{\lambda}{\mu}\right)^{n+m}p_0 \\ \sum\limits_{i=0}^{n}\frac{1}{i!}\left(\frac{\lambda}{\mu}\right)^i p_0+\sum\limits_{i=n+1}^{n+m}\frac{1}{n!n^{i-n}}\left(\frac{\lambda}{\mu}\right)^i p_0=1 \end{cases}} Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Leftrightarrow} Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{cases}p_0=\left(\sum\limits_{i=0}^{n}\frac{\lambda^i}{i!\mu^i}+\sum\limits_{i=n+1}^{n+m}\frac{\lambda^i}{n!n^{i-n}\mu^i}\right)^{-1} \\ p_1=\frac{\lambda}{\mu}p_0 \\ \ldots \\ p_i=\frac{\lambda^i}{i!\mu^i}p_0 \\ \ldots \\ p_n=\frac{\lambda^n}{n!\mu^n}p_0 \\ p_{n+1}=\frac{\lambda^{n+1}}{n!n\mu^{n+1}}p_0 \\ \ldots \\ p_{n+m-1}=\frac{\lambda^{n+m-1}}{n!n^{m-1}\mu^{n+m-1}}p_0 \\ p_{n+m}=\frac{\lambda^{n+m}}{n!n^m\mu^{n+m}}p_0 \end{cases}}

В результате получаем решение системы: Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_0=\frac{1}{\sum\limits_{i=0}^{n}\frac{\lambda^i}{i!\mu^i}+\sum\limits_{i=n+1}^{n+m}\frac{\lambda^i}{n!n^{i-n}\mu^i}}, \ p_i=\frac{\lambda^i}{i!\mu^i} p_0 , \forall i\in N_n, \ p_{n+i}=\frac{\lambda^{n+i}}{n!n^i\mu^{n+i}} p_0 , \forall i\in N_m }

Основные характеристики системы

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle t_\lambda=\frac{1}{\lambda}, t_\mu=\frac{1}{\mu}, \rho=\frac{\lambda}{\mu}, \chi=\frac{\lambda}{n\mu},}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_0=\frac{1}{\sum\limits_{i=0}^{n}\frac{\rho^i}{i!}+ \frac{\rho^n}{n!} \sum\limits_{i=1}^{m}\frac{\rho^i}{n^i}}= \frac{1}{1+\frac{\rho}{1!}+\frac{\rho^2}{2!}+\ldots+\frac{\rho^n}{n!}+ \frac{\rho^{n+1}}{n!n}+\frac{\rho^{n+2}}{n!n^2}+\ldots+\frac{\rho^{n+m}}{n!n^m}}, p_i=\frac{\rho^i}{i!} p_0 , \forall i\in N_n, p_{n+i}=\frac{\rho^{n+i}}{n!n^i} p_0=\frac{\rho^i}{n^i} p_n=\chi^ip_n, \forall i\in N_m,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar s={\sum\limits_{i=0}^{n}{ip_i}+\sum\limits_{i=1}^{m}{np_{n+i}}}=\rho(1-p_{n+m})=\rho\left(1-\chi^mp_n\right), \bar r=\sum\limits_{i=1}^{m}{ip_{n+i}}=\sum\limits_{i=1}^{m}{i\chi^ip_n }, \bar l=\bar s+\bar r=\sum\limits_{i=1}^{n+m}{ip_i }=\rho\left(1-\chi^mp_n\right)+ \sum\limits_{i=1}^{m}{i\chi^ip_n}, \bar k=\bar s,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle q=1-p_{n+m}=1-\chi^mp_n, A=\lambda(1-p_{n+m})=\lambda\left(1-\chi^mp_n\right),}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_\text{прост.}=p_0, p_\text{отк.}=p_{n+m}=\chi^mp_n, p_\text{обсл.}=1-p_{n+m}=1-\chi^mp_n, }

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_\text{п.загр.}=\sum\limits_{i=0}^mp_{n+i}=\sum\limits_{i=0}^m\chi^i p_n, p_\text{н.загр.}=\sum\limits_{i=0}^{n-1}p_i=\sum\limits_{i=0}^{n-1}\frac{\rho^i}{i!}p_0, =1-p_n=1-\frac{\rho^n}{n!}p_0, p_\text{н.очер.} =\sum\limits_{i=1}^mp_{n+i}=\sum\limits_{i=1}^m\chi^i p_n, }

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_\text{1зан.}=\frac{\bar k}{n}=\chi\left(1-\chi^mp_n\right), p_\text{1прост.}=1-\frac{\bar k}{n}=1-\chi\left(1-\chi^mp_n\right), }

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{н.очер.}=\bar t_\lambda\cdot\frac{\sum\limits_{i=1}^mp_{n+i}}{p_n}=\frac{\sum\limits_{i=1}^m\chi^i}{\lambda}, \bar t_\text{н.загр.}=\bar t_{n\mu}\cdot\frac{\sum\limits_{i=0}^{n-1}p_i}{p_n}=\frac{\sum\limits_{i=0}^{n-1}\frac{\rho^i}{i!}}{n\mu\frac{\rho^n}{n!}},}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{п.загр.}= \bar t_\text{н.загр.}\cdot\frac{p_\text{п.загр.}}{p_\text{н.загр.}}=\frac{\sum\limits_{i=0}^m\chi^i}{n\mu}, \bar t_\text{1зан.}= \bar t_\mu+p_\text{н.очер.}\cdot\bar t_\text{н.очер.}= \frac{1}{\mu}+\frac{1}{\lambda }\left(\sum\limits_{i=1}^m\chi_i\right)^2p_n,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{1прост.}= \bar t_\text{1зан.}\cdot\frac{p_\text{1прост.}}{p_\text{1зан.}}=\left[\frac{1}{\mu}+\frac{1}{\lambda }\left(\sum\limits_{i=1}^m\chi_i\right)^2p_n\right] \cdot\frac{1-\chi\left(1-\chi^mp_n\right)}{\chi\left(1-\chi^mp_n\right)}, }

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{прост.}= \bar t_\lambda=\frac{1}{\lambda}, \bar t_\text{обсл.}= \bar t_\lambda\cdot\bar s=\frac{\bar s }{\lambda}, \bar t_\text{очер.}= \bar t_\lambda\cdot\bar r=\frac{\bar r }{\lambda}, \bar t_\text{сист.}= \bar t_\lambda\cdot\bar l=\frac{\bar l}{\lambda}.}

При χ≠1 получаем

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_0=\frac{1}{1+\frac{\rho}{1!}+\frac{\rho^2}{2!}+\ldots+\frac{\rho^{n-1}}{(n-1)!}+\frac{\rho^n}{n!}\cdot\frac{1-\chi^{m+1}}{1-\chi}},p_i=\frac{\rho^i}{i!}p_0,\forall i\in N_n,p_{n+i}=\chi^ip_n,\forall i\in N_m,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar s=\rho\left(1-\chi^mp_n\right),\bar r=\frac{1-(m+1)\chi^m+m\chi^{m+1}}{\left(1-\chi\right)^2}\chi p_n,\bar l=\bar s+\bar r=\rho\left(1-\chi^mp_n\right)+\frac{1-(m+1)\chi^m+m\chi^{m+1}}{\left(1-\chi\right)^2}\chi p_n,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar k=\rho\left(1-\chi^mp_n\right),q=1-\chi^mp_n, A=\lambda\left(1-\chi^mp_n\right),}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_\text{прост.}=p_0, p_\text{отк.}=\chi^mp_n, p_\text{обсл.}=1-\chi^mp_n, }

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_\text{п.загр.}=\frac{1-\chi^{m+1}}{1-\chi }p_n, p_\text{н.загр.}=1-\frac{1-\chi^{m+1}}{1-\chi}p_n, p_\text{н.очер.}=\frac{1-\chi^m}{1-\chi}\chi p_n, p_\text{1зан.}= \chi\left(1-\chi^mp_n\right), p_\text{1прост.}=1-\chi\left(1-\chi^mp_n\right), }

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{н.очер.}=\frac{\chi\left(1-\chi^m\right)}{\lambda\left(1-\chi\right)}=\frac{1-\chi^m}{n\mu\left(1-\chi\right)},\bar t_\text{н.загр.}=\frac{1+\frac{\rho}{1!}+\frac{\rho^2}{2!}+\ldots+\frac{\rho^{n-1}}{(n-1)!}}{n\mu\frac{\rho^n}{n!}},}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{п.загр.}=\frac{1-\chi^{m+1}}{n\mu\left(1-\chi\right)},\bar t_\text{1зан.}=\frac{1}{\mu}+\frac{\chi^2\left(1-\chi^m\right)^2}{\lambda\left(1-\chi\right)^2}p_n=\frac{1}{\mu}+\frac{\chi\left(1-\chi^m\right)^2}{n\mu\left(1-\chi\right)^2}p_n,\bar t_\text{1прост.}=\bar t_\text{1зан.}\cdot\frac{1-\chi\left(1-\chi^mp_n\right)}{\chi\left(1-\chi^mp_n\right)},}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{прост.}=\bar t_\lambda=\frac{1}{\lambda},\bar t_\text{обсл.}=\frac{1-\chi^mp_n}{\mu},\bar t_\text{очер.}=\frac{1-(m+1)\chi^m+m\chi^{m+1}}{n\mu\left(1-\chi\right)^2}p_n,\bar t_\text{сист.}=\bar t_\text{обсл.}+\bar t_\text{очер.}=\frac{1-\chi^mp_n}{\mu}+ \frac{1-(m+1)\chi^m+m\chi^{m+1}}{n\mu\left(1-\chi\right)^2}p_n.}

При χ=1 получаем

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \chi=1\Leftrightarrow \lambda=n\mu\Leftrightarrow\rho=n,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_0=\frac{1}{1+\frac{\rho}{1!}+\frac{\rho^2}{2!}+\ldots+\frac{\rho^n}{n!}+m\frac{\rho^n}{n!}},p_i=\frac{\rho^i}{i!} p_0 ,\forall i\in N_n, p_{n+i}= p_n=\frac{\rho^n}{n!}p_0,\forall i\in N_m,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar s=\rho(1-p_n),\bar r=\frac{m(m+1)}{2}p_n,\bar l=\bar s+\bar r=\rho(1-p_n)+\frac{m(m+1)}{2}p_n,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar k=\bar s=\rho(1-p_n), q=1-p_n, A=\lambda(1-p_n),}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_\text{прост.}=p_0, p_\text{отк.}=p_n, p_\text{обсл.}=1-p_n,}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_\text{п.загр.}=(m+1)p_n, p_\text{н.загр.}=1-(m+1)p_n, p_\text{н.очер.}=mp_n, p_\text{1зан.}=1-p_n, p_\text{1прост.}=p_n, }

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{н.очер.}=\frac{m}{\lambda}, \bar t_\text{п.загр.}=\frac{m+1}{n\mu},\bar t_\text{н.загр.}= \frac{1-(m+1)p_n}{n\mu p_n},}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{1зан.}=\frac{1}{\mu }+\frac{m^2}{\lambda}p_n, \bar t_\text{1прост.}=\left(\frac{1}{\mu}+\frac{m^2}{\lambda }p_n\right)\cdot\frac{p_n}{1-p_n}, }

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar t_\text{прост.}= \bar t_\lambda=\frac{1}{\lambda},\bar t_\text{обсл.}= \frac{\rho(1-p_n)}{\lambda}=\frac{1-p_n}{\mu}, \bar t_\text{очер.}= \frac{m(m+1)}{2\lambda}p_n, \bar t_\text{сист.}=\frac{1-p_n}{\mu}+\frac{m(m+1)}{2\lambda}p_n.}

• Заметим, что при n=1 СМО с очередью становится одноканальной.

Другие СМО

• СМО с отказами;
• СМО с ограниченным временем ожидания;
• СМО замкнутая с очередью;
• СМО с взаимопомощью с очередью;
• СМО с отказами и взаимопомощью;
• СМО с бесконечным числом каналов;
• СМО с бесконечной очередью;
• СМО замкнутая без очереди.

Литература

• Овчаров Л. А. Прикладные задачи теории массового обслуживания, «Машиностроение», М.,1969.