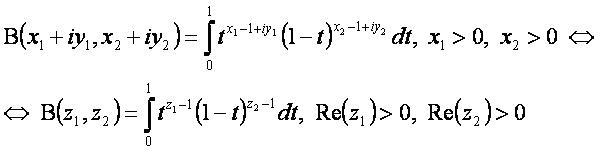Бета-функция

Интеграл Эйлера I рода

Факториал дробного числа. Гамма-функция и бета-функция // Точки Лагранжа [56:21]

Бета-функция — это специальная функция от двух комплексных переменных, имеющая интегральное представление:

$B(x_{1}+iy_{1},x_{2}+iy_{2})=\int \limits _{0}^{1}t^{x_{1}-1+iy_{1}}(1-t)^{x_{2}-1+iy_{2}}dt,\ x_{1}>0,\ x_{2}>0$.

Обозначения:

x₁ = Re(z₁) — действительная часть (абсцисса) первого числа;

y₁ = Im(z₁) — мнимая часть (ордината) первого числа;

x₂ = Re(z₂) — действительная часть (абсцисса) второго числа;

y₂ = Im(z₂) — мнимая часть (ордината) второго числа;

z₁ = x₁ + iy₁ — первое комплексное число;

z₂ = x₂ + iy₂ — второе комплексное число;

t — параметр интегрирования;

φ — параметр интегрирования;

Г(z) — гамма-функция;

B(z₁,z₂) — бета-функция.

Формулы:

Интеграл Эйлера I рода

$B(x_{1}+iy_{1},x_{2}+iy_{2})=\int \limits _{0}^{1}t^{x_{1}-1+iy_{1}}(1-t)^{x_{2}-1+iy_{2}}dt,\ x_{1}>0,\ x_{2}>0\Leftrightarrow$

$\Leftrightarrow B(z_{1},z_{2})=\int \limits _{0}^{1}t^{z_{1}-1}(1-t)^{z_{2}-1}dt,\ Re(z_{1})>0,\ Re(z_{2})>0$

Интегральное представление

$B(x_{1}+iy_{1},x_{2}+iy_{2})=\int \limits _{0}^{\infty }{\frac {t^{x_{1}-1+iy_{1}}}{(1+t)^{x_{1}+iy_{1}+x_{2}+iy_{2}}}}dt,\ x_{1}>0,\ x_{2}>0\Leftrightarrow$

$\Leftrightarrow B(z_{1},z_{2})=\int \limits _{0}^{\infty }{\frac {t^{z_{1}-1}}{(1+t)^{z_{1}+z_{2}}}}dt,\ Re(z_{1})>0,\ Re(z_{2})>0$

$\Leftrightarrow B(z_{1},z_{2})=2\int \limits _{0}^{\frac {\pi }{2}}\sin ^{2z_{1}-1}\varphi \cos ^{2z_{2}-1}\varphi d\varphi ,\ Re(z_{1})>0,\ Re(z_{2})>0$

Свойства:

$B(x_{1}+iy_{1},x_{2}+iy_{2})={\frac {\Gamma (x_{1}+iy_{1})\Gamma (x_{2}+iy_{2})}{\Gamma (x_{1}+iy_{1}+x_{2}+iy_{2})}}\Leftrightarrow B(z_{1},z_{2})={\frac {\Gamma (z_{1})\Gamma (z_{2})}{\Gamma (z_{1}+z_{2})}}$

$B(x_{1}+iy_{1},x_{2}+iy_{2})=B(x_{2}+iy_{2},x_{1}+iy_{1})\Leftrightarrow B(z_{1},z_{2})=B(z_{2},z_{1})$

$B(x_{1}+iy_{1},x_{2}+iy_{2})B(x_{1}+iy_{1}+x_{2}+iy_{2},x_{3}+iy_{3})=$

$=B(x_{2}+iy_{2},x_{3}+iy_{3})B(x_{2}+iy_{2}+x_{3}+iy_{3},x_{1}+iy_{1})\Leftrightarrow$

$\Leftrightarrow B(z_{1},z_{2})B(z_{1}+z_{2},z_{3})=B(z_{2},z_{3})B(z_{2}+z_{3},z_{1})$

Примеры:

$B(n_{1},n_{2})={\frac {\Gamma (n_{1})\Gamma (n_{2})}{\Gamma (n_{1}+n_{2})}},\ n_{1}\in \mathbb {N} ,\ n_{2}\in \mathbb {N} \Leftrightarrow$

$\Leftrightarrow B(n_{1},n_{2})={\frac {(n_{1}-1)!(n_{2}-1)!}{(n_{1}+n_{2}-1)!}},\ n_{1}\in \mathbb {N} ,\ n_{2}\in \mathbb {N}$

$B\left(n_{1}+{\frac {1}{2}},n_{2}+{\frac {1}{2}}\right)={\frac {\Gamma \left(n_{1}+{\frac {1}{2}}\right)\Gamma \left(n_{2}+{\frac {1}{2}}\right)}{\Gamma (n_{1}+n_{2}+1)}},\ n_{1}\in \mathbb {N} ,\ n_{2}\in \mathbb {N} \Leftrightarrow$

$\Leftrightarrow B\left(n_{1}+{\frac {1}{2}},n_{2}+{\frac {1}{2}}\right)={\frac {(2n_{1}-1)!!(2n_{2}-1)!!}{2^{n_{1}+n_{2}}(n_{1}+n_{2})!}}\pi ,\ n_{1}\in \mathbb {N} ,\ n_{2}\in \mathbb {N}$

$B\left({\frac {1}{2}}+n,{\frac {1}{2}}-n\right)=\Gamma \left({\frac {1}{2}}+n\right)\Gamma \left({\frac {1}{2}}-n\right),\ n\in \mathbb {N} \Leftrightarrow$

$\Leftrightarrow B\left({\frac {1}{2}}+n,{\frac {1}{2}}-n\right)=(-1)^{n}\pi$

См. также

• Бета-распределение

Другие функции:

• интегральный синус;
• интегральный косинус;
• интегральная показательная функция;
• интегральный логарифм;
• гамма-функция;
• бета-функция;
• неполная гамма-функция;
• неполная бета-функция.

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970, стр.638.