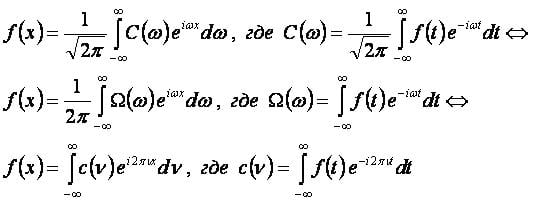Комплексный интеграл Фурье

Формулы

Интеграл Фурье комплексный — это интеграл, представляющий в комплексной форме функцию f(x) на интервале (−∞, ∞).

Формулы:

Представление функции f(x) на интервале (−∞; ∞):

$f(x)={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }C(\omega )e^{i\omega x}d\omega$, где $C(\omega )={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }f(t)e^{-i\omega t}dt\Leftrightarrow$

$f(x)={\frac {1}{2\pi }}\int \limits _{-\infty }^{\infty }\Omega (\omega )e^{i\omega x}d\omega$, где $\Omega (\omega )=\int \limits _{-\infty }^{\infty }f(t)e^{-i\omega t}dt\Leftrightarrow$

$f(x)=\int \limits _{-\infty }^{\infty }c(\nu )e^{2\pi i\nu x}d\nu$, где $c(\nu )=\int \limits _{-\infty }^{\infty }f(t)e^{-i2\pi \nu t}dt$

• Коэффициент C(ω) называется преобразованием Фурье функции f(x).

См. также

• Комплексный ряд Фурье

Другие интегралы:

• интеграл;
• интегралы элементарных функций;
• интегралы дробно-рациональных функций;
• интегралы функций с корнями;
• интегралы тригонометрических функций;
• интегралы обратных тригонометрических функций;
• интегралы гиперболических функций;
• интегралы обратных гиперболических функций;
• интеграл Фурье;
• интеграл Фурье комплексный;
• эллиптические интегралы;
• интегралы, определяемые методом замены переменных;
• интегралы, определяемые по интегральным равенствам;
• интегралы, определяемые по интегральным формулам;
• интеграл Эйлера-Пуассона.

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970.
• Бермант А. Ф., Араманович И. Г. Краткий курс математического анализа для втузов — М.: Наука, 1973.