VIDEO
Полезные мелочи / Гамма-функция / 1 // Павел Шестопалов [6:16]
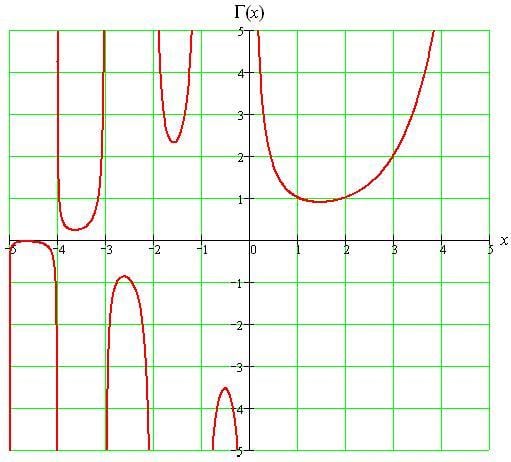
Гамма-функция — специальная функция от комплексной переменной, имеющая интегральное представление.
Гамма-функция [ править ] x = Re(z) — действительная часть (абсцисса) числа;
y = Im(z) — мнимая часть (ордината) числа;
z = x + iy — аргумент — комплексного числа ;
Г(z) — гамма-функция.
Гамма-функция имеет интегральное представление, для положительной действительной части аргумента в виде интеграла Эйлера второго рода, для отрицательной действительной части — интегральное представление Ганкеля.
Интеграл Эйлера II рода [ править ] Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Gamma(x+iy)=\int\limits_0^\infty t^{x-1+iy}e^{-t}dt, \ x > 0 \Leftrightarrow \Gamma(z) = \int\limits_0^\infty t^{z-1}e^{-t}dt, \ Re(z) > 0}
Интегральное представление Ганкеля [ править ]
Γ
(
x
+
i
y
)
=
2
π
i
∮
C
t
−
x
−
i
y
e
t
d
t
,
x
<
0
⇔
Γ
(
z
)
=
2
π
i
∮
C
t
−
z
e
t
d
t
,
R
e
(
z
)
<
0
{\displaystyle \Gamma (x+iy)={\frac {2\pi i}{\oint \limits _{C}t^{-x-iy}e^{t}dt}},\ x<0\Leftrightarrow \Gamma (z)={\frac {2\pi i}{\oint \limits _{C}t^{-z}e^{t}dt}},\ Re(z)<0}
C — контур идёт из -∞ по отрицательной части действительной оси, обходит начало координат в положительном направлении (против часовой стрелки) и опять по отрицательной части оси абсцисс возвращается к исходной точке.
Γ
(
x
+
i
y
)
=
(
x
−
1
+
i
y
)
Γ
(
x
−
1
+
i
y
)
⇔
Γ
(
z
)
=
(
z
−
1
)
Γ
(
z
−
1
)
{\displaystyle \Gamma (x+iy)=(x-1+iy)\Gamma (x-1+iy)\Leftrightarrow \Gamma (z)=(z-1)\Gamma (z-1)}
Γ
(
x
+
1
+
i
y
)
=
(
x
+
i
y
)
Γ
(
x
+
i
y
)
⇔
Γ
(
z
+
1
)
=
z
Γ
(
z
)
{\displaystyle \Gamma (x+1+iy)=(x+iy)\Gamma (x+iy)\Leftrightarrow \Gamma (z+1)=z\Gamma (z)}
Γ
(
x
+
i
y
)
Γ
(
1
−
x
−
i
y
)
=
π
sin
[
π
(
x
+
i
y
)
]
⇔
Γ
(
z
)
Γ
(
1
−
z
)
=
π
sin
(
π
z
)
{\displaystyle \Gamma (x+iy)\Gamma (1-x-iy)={\frac {\pi }{\sin \left[\pi (x+iy)\right]}}\Leftrightarrow \Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin(\pi z)}}}
Γ
(
1
2
+
x
+
i
y
)
Γ
(
1
2
−
x
−
i
y
)
=
π
cos
[
π
(
x
+
i
y
)
]
⇔
Γ
(
1
2
+
z
)
Γ
(
1
2
−
z
)
=
π
cos
(
π
z
)
{\displaystyle \Gamma \left({\frac {1}{2}}+x+iy\right)\Gamma \left({\frac {1}{2}}-x-iy\right)={\frac {\pi }{\cos \left[\pi (x+iy)\right]}}\Leftrightarrow \Gamma \left({\frac {1}{2}}+z\right)\Gamma \left({\frac {1}{2}}-z\right)={\frac {\pi }{\cos(\pi z)}}}
Γ
(
n
)
=
(
n
−
1
)
!
,
n
∈
N
⇔
Γ
(
1
)
=
1
{\displaystyle \Gamma (n)=(n-1)!,\ n\in \mathbb {N} \Leftrightarrow \Gamma (1)=1}
Γ
(
2
)
=
1
{\displaystyle \Gamma (2)=1}
Γ
(
3
)
=
2
{\displaystyle \Gamma (3)=2}
Γ
(
4
)
=
6
{\displaystyle \Gamma (4)=6}
Γ
(
5
)
=
24
{\displaystyle \Gamma (5)=24}
Γ
(
6
)
=
120
{\displaystyle \Gamma (6)=120}
Γ
(
7
)
=
720
,
…
{\displaystyle \Gamma (7)=720,\ldots }
Γ
(
1
2
)
=
π
{\displaystyle \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}}
Γ
(
1
2
+
n
)
=
(
2
n
−
1
)
!
!
2
n
π
,
n
∈
N
⇔
Γ
(
1
2
+
n
)
=
(
2
n
)
!
4
n
n
!
π
,
n
∈
N
⇔
{\displaystyle \Gamma \left({\frac {1}{2}}+n\right)={\frac {(2n-1)!!}{2^{n}}}{\sqrt {\pi }},\ n\in \mathbb {N} \Leftrightarrow \Gamma \left({\frac {1}{2}}+n\right)={\frac {(2n)!}{4^{n}n!}}{\sqrt {\pi }},\ n\in \mathbb {N} \Leftrightarrow }
⇔
Γ
(
3
2
)
=
π
2
{\displaystyle \Leftrightarrow \Gamma \left({\frac {3}{2}}\right)={\frac {\sqrt {\pi }}{2}}}
Γ
(
5
2
)
=
3
π
4
{\displaystyle \Gamma \left({\frac {5}{2}}\right)={\frac {3{\sqrt {\pi }}}{4}}}
Γ
(
7
2
)
=
15
π
8
{\displaystyle \Gamma \left({\frac {7}{2}}\right)={\frac {15{\sqrt {\pi }}}{8}}}
Γ
(
9
2
)
=
105
π
16
{\displaystyle \Gamma \left({\frac {9}{2}}\right)={\frac {105{\sqrt {\pi }}}{16}}}
Γ
(
11
2
)
=
945
π
32
{\displaystyle \Gamma \left({\frac {11}{2}}\right)={\frac {945{\sqrt {\pi }}}{32}}}
Γ
(
13
2
)
=
10395
π
64
{\displaystyle \Gamma \left({\frac {13}{2}}\right)={\frac {10395{\sqrt {\pi }}}{64}}}
Γ
(
15
2
)
=
135135
π
128
,
…
{\displaystyle \Gamma \left({\frac {15}{2}}\right)={\frac {135135{\sqrt {\pi }}}{128}},\ldots }
Γ
(
1
2
−
n
)
=
(
−
2
)
n
(
2
n
−
1
)
!
!
π
,
n
∈
N
⇔
Γ
(
1
2
−
n
)
=
(
−
4
)
n
n
!
(
2
n
)
!
π
,
n
∈
N
⇔
{\displaystyle \Gamma \left({\frac {1}{2}}-n\right)={\frac {(-2)^{n}}{(2n-1)!!}}{\sqrt {\pi }},\ n\in \mathbb {N} \Leftrightarrow \Gamma \left({\frac {1}{2}}-n\right)={\frac {(-4)^{n}n!}{(2n)!}}{\sqrt {\pi }},\ n\in \mathbb {N} \Leftrightarrow }
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Leftrightarrow\Gamma\left(-\frac{1}{2}\right)=-2\sqrt{\pi}}
,
Γ
(
−
3
2
)
=
4
π
3
{\displaystyle \Gamma \left(-{\frac {3}{2}}\right)={\frac {4{\sqrt {\pi }}}{3}}}
Γ
(
−
5
2
)
=
−
8
π
15
{\displaystyle \Gamma \left(-{\frac {5}{2}}\right)=-{\frac {8{\sqrt {\pi }}}{15}}}
Γ
(
−
7
2
)
=
16
π
105
{\displaystyle \Gamma \left(-{\frac {7}{2}}\right)={\frac {16{\sqrt {\pi }}}{105}}}
Γ
(
−
9
2
)
=
32
π
945
{\displaystyle \Gamma \left(-{\frac {9}{2}}\right)={\frac {32{\sqrt {\pi }}}{945}}}
Γ
(
−
11
2
)
=
−
64
π
10395
{\displaystyle \Gamma \left(-{\frac {11}{2}}\right)=-{\frac {64{\sqrt {\pi }}}{10395}}}
Γ
(
−
13
2
)
=
128
π
135135
,
…
{\displaystyle \Gamma \left(-{\frac {13}{2}}\right)={\frac {128{\sqrt {\pi }}}{135135}},\ldots }
Γ
(
1
2
+
n
)
Γ
(
1
2
−
n
)
=
(
−
1
)
n
π
,
n
∈
N
{\displaystyle \Gamma \left({\frac {1}{2}}+n\right)\Gamma \left({\frac {1}{2}}-n\right)=(-1)^{n}\pi ,\ n\in \mathbb {N} }
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970, стр.633.
Полезные мелочи / Гамма-функция / 1 // Павел Шестопалов [6:16]
![{\displaystyle \Gamma (x+iy)\Gamma (1-x-iy)={\frac {\pi }{\sin \left[\pi (x+iy)\right]}}\Leftrightarrow \Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin(\pi z)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f34bc834be16e811a1346b4d99f473e052c70bf7)
![{\displaystyle \Gamma \left({\frac {1}{2}}+x+iy\right)\Gamma \left({\frac {1}{2}}-x-iy\right)={\frac {\pi }{\cos \left[\pi (x+iy)\right]}}\Leftrightarrow \Gamma \left({\frac {1}{2}}+z\right)\Gamma \left({\frac {1}{2}}-z\right)={\frac {\pi }{\cos(\pi z)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a0aad82c859d6e3e52c85636ccdeb13164ca91f)
