Интеграл
Интеграл, в математике — непрерывная сумма произведений значений подынтегральной функции на дифференциал аргумента.
Интеграл от функции[править]
Нахождение интеграла от функции называется интегрированием. При интегрировании подынтегральной функции находят первообразную функцию, производная от которой равна подынтегральной функции. Интеграл от функции может быть неопределённым, а может быть определённым.
Суть неопределённого интеграла это класс функций (первообразная плюс константа), отличающихся только константой, производная которых равна подынтегральной функции.
Суть определённого интеграла это некое число, равное непрерывной алгебраической сумме произведений значений подынтегральной функции на дифференциал аргумента.
Для положительных подынтегральных функций определённый интеграл равен величине площади криволинейной трапеции, ограниченной графиком функции, осью абсцисс и пределами интегрирования.
Неопределённый интеграл от функции[править]
Неопределённый интеграл от функции определяется по формуле:
- ∫f(x)dx = F(x) + C, где F'(x) = f(x)
f(x) — подынтегральная функция,
F(x) — первообразная функция.
C — константа.
Свойства неопределённых интегралов[править]
Для функций u = f(x) и v = g(x) верны правила:
При f(x) и g(x) = C1 получаем:
При f(x) = C1 и g(x) получаем:
Интегрирование по частям[править]
Для функций u = f(x) и v = g(x) верно правило:
Примеры неопределённых интегралов[править]
- интегралы элементарных функций;
- интегралы тригонометрических функций;
- интегралы функций с корнями;
- метод замены переменных.
Определённый интеграл от функции[править]
Определённый интеграл от функции определяется по формуле Ньютона-Лейбница:
- ,
где производная
f(x) — подынтегральная функция,
F(x) — первообразная функция.
- Примеры определённых интегралов
Любой определённый интеграл можно вычислить или оценить с помощью формул численного интегрирования.
См. также[править]
Другие интегралы:[править]
- интеграл;
- интегралы элементарных функций;
- интегралы дробно-рациональных функций;
- интегралы функций с корнями;
- интегралы тригонометрических функций;
- интегралы обратных тригонометрических функций;
- интегралы гиперболических функций;
- интегралы обратных гиперболических функций;
- интеграл Фурье;
- интеграл Фурье комплексный;
- эллиптические интегралы;
- интегралы, определяемые методом замены переменных;
- интегралы, определяемые по интегральным равенствам;
- интегралы, определяемые по интегральным формулам;
- интеграл Эйлера-Пуассона.
Другие понятия[править]
Литература[править]
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
![{\displaystyle {\begin{cases}\int [f(x)+g(x)]dx=\int f(x)dx+\int g(x)dx\\\int [f(x)-g(x)]dx=\int f(x)dx-\int g(x)dx\end{cases}}\Leftrightarrow {\begin{cases}\int (u+v)dx=\int udx+\int vdx\\\int (u-v)dx=\int udx-\int vdx\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18d8f31cc3ca059fdde74edf5e547202806b115f)
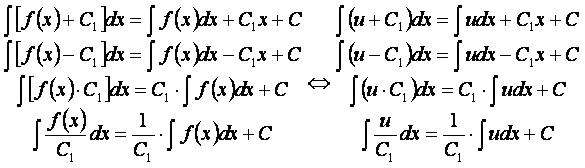
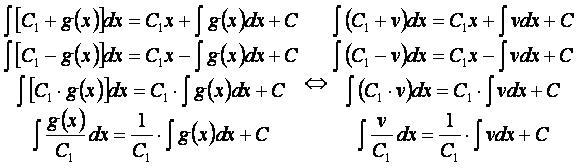
![{\displaystyle {\begin{cases}\int [f(x)g'(x)]dx=f(x)\cdot g(x)-\int [f'(x)g(x)]dx\\\int f(x)dg(x)=f(x)\cdot g(x)-\int g(x)df(x)\end{cases}}\Leftrightarrow {\begin{cases}\int (uv')dx=u\cdot v-\int (u'v)dx\\\int udv=u\cdot v-\int vdu\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/222e0521cc1ff6eb4739e54fa870cc12ac93b90a)


