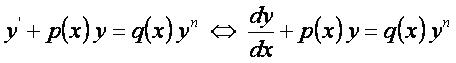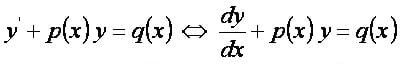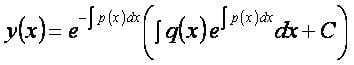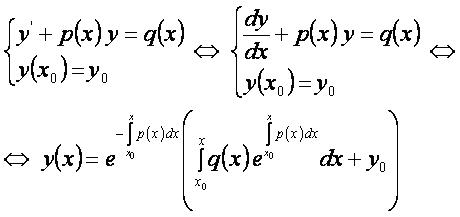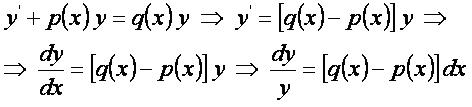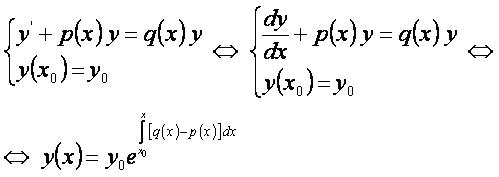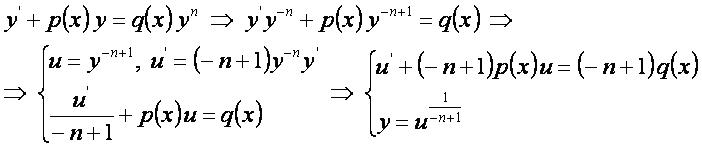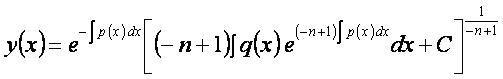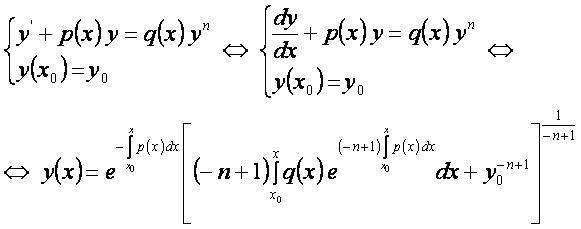Дифференциальное уравнение Бернулли

Дифференциальные уравнения Бернулли — это уравнения вида y^’+p(x)y=q(x)yⁿ.

Обозначения

x – переменная - аргумент функции;

y – переменная – функция;

y^’ – производная функции;

y^’=f(x,y) – общий вид дифференциального уравнения, разрешённого относительно производной.

Дифференциальное уравнение

Линейное

При n=0 – это линейное дифференциальное уравнение.

Общее решение

Частное решение

С разделяющимися переменными

При n=1 – это дифференциальное уравнение с разделяющимися переменными.

Общее решение

Частное решение

Сводящееся к линейному

При n≠1 – дифференциальное уравнение сводится к линейному.

Общее решение

Частное решение

Другие дифференциальные уравнения

• с разделяющимися переменными;
• однородное;
• линейное;
• уравнение Бернулли;
• уравнение в полных дифференциалах;
• уравнение Клеро;
• уравнение второго порядка, не содержащее y и y^’;
• уравнение второго порядка, не содержащее y;
• уравнение второго порядка, не содержащее x;
• однородное уравнение второго порядка с постоянными коэффициентами;
• неоднородное уравнение второго порядка с постоянными коэффициентами;
• уравнение n-ого порядка, содержащее только переменную x;
• однородное уравнение n-ого порядка с постоянными коэффициентами;
• неоднородное уравнение n-ого порядка с постоянными коэффициентами;
• общее дифференциальное уравнение.

Литература

• Бермант А. Ф., Араманович И. Г. Краткий курс математического анализа для втузов — М.: Наука, 1973, стр.538.

Ссылки

• Участник:Logic-samara