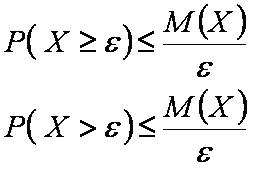Неравенство Маркова

Неравенство Маркова

62. Неравенство Маркова (Андрей Михайлович Райгородский [27:00]

Неравенство Маркова — неравенство, гласящее: вероятность того, что непрерывная положительная случайная величина превысит некоторое положительное число, не более отношения её математического ожидания к заданному числу. Открыто А. А. Марковым (старшим), названо в честь него же.

Обозначения

X — непрерывная положительная случайная величина;

M(X) — математическое ожидание положительной случайной величины X;

ε — положительное число большее чем M(X).

Формула неравенства

$P(X\geqslant \varepsilon )\leqslant {\frac {M(X)}{\varepsilon }}$

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle P(X>\varepsilon )\leqslant {\frac {M(X)}{\varepsilon }}}

• Заметим, что вероятность равенства для непрерывной случайной величины равна нулю, поэтому строгое и нестрогое неравенства равнозначны.

Доказательство для НСВ

Доказательство неравенства Маркова для непрерывной случайной величины

• Неравенство Маркова применимо для дискретной положительной случайной величины X в виде:

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle P(X>\varepsilon )\leqslant {\frac {M(X)}{\varepsilon }}}

Доказательство для ДСВ

Доказательство неравенства Маркова для дискретной случайной величины

Следствие

$P(X<\varepsilon )\geqslant 1-{\frac {M(X)}{\varepsilon }}$

$P(X\leqslant \varepsilon )\geqslant 1-{\frac {M(X)}{\varepsilon }}$

• Следствие неравенства Маркова применимо для дискретной положительной случайной величины X только в виде:

$P(X\leqslant \varepsilon )\geqslant 1-{\frac {M(X)}{\varepsilon }}$

Другие неравенства:

1. неравенство n-степени числа;
2. неравенство n-факториала и среднего арифметического;
3. неравенство n-факториала и среднего квадратического;
4. неравенство n-факториала и среднего кубического;
5. неравенство n-факториала и n-степени двух;
6. неравенство r-степени числа;
7. неравенство Бернулли;
8. неравенство произведения единицы со степенью числа и степени единицы с числом;
9. неравенство произведения отношений нечётных к чётным натуральным числам;
10. неравенство степеней n и n+1 для чисел;
11. неравенство степеней n и n+1 для единиц с обратными числами;
12. неравенство суммы n-степеней единицы без дроби и единицы с дробью;
13. неравенство суммы обратных квадратов n натуральных чисел;
14. неравенство суммы обратных корней n натуральных чисел со знаком больше;
15. неравенство суммы обратных корней n натуральных чисел со знаком меньше;
16. неравенство суммы обратных n натуральных чисел, начиная с числа n+1;
17. неравенство трёх квадратов;
18. неравенство трёх кубов;
19. неравенство трёх попарных отношений;
20. неравенство факториала нечётного числа;
21. неравенство факториала чётного числа;
22. обобщённое неравенство Бернулли;
23. неравенство Маркова;
24. неравенство Чебышёва.

Литература

• Кремер Н. Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2004, стр.223-224.