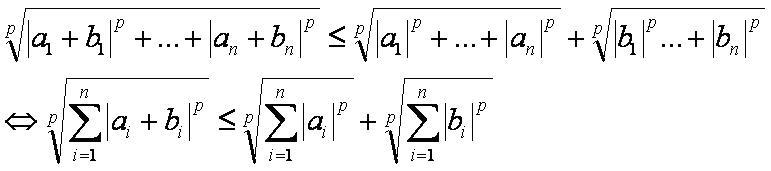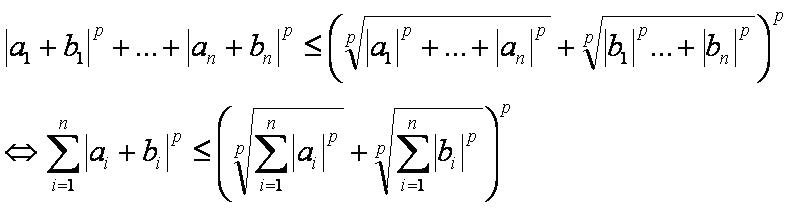Неравенство Минковского

Неравенство Минковского — неравенство, гласящее, что корень p-степени из суммы p-степеней модулей сумм каждой пары n чисел с другими n числами не больше суммы корней p-степени из сумм p-степеней модулей всех первых элементов пар и вторых элементов пар.

Названо в честь первооткрывателя — Германа Минковского.

Обозначения

n – число чисел в наборах;

p – число большее или равное 1;

$a_{i}$ – i-ое число;

$b_{i}$ – i-ое число.

Формула неравенства

• Если множества чисел $\{a_{i}\}$ и $\{b_{i}\}$ считать векторами n-мерного пространства, то неравенство Минковского означает, что p-норма суммы векторов не более суммы p-норм векторов.

Следствие

Другие неравенства:

• неравенство Коши;
• неравенство Коши-Буняковского;
• интегральное неравенство Коши-Буняковского;
• неравенство Минковского;
• интегральное неравенство Минковского;
• неравенство Гёльдера;
• интегральное неравенство Гёльдера;
• неравенство Фань Цзы;
• неравенство Маркова;
• неравенство Чебышёва.

См. также

• Неравенство Гёльдера и Минковского для конечных и бесконечных сумм
• Герман Минковский

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970.

Ссылки

• Участник:Logic-samara